Professor James P. Vary from the Department of Physics and Astronomy at Iowa State University explains how supercomputers are revolutionising weather forecasts and predictive science.
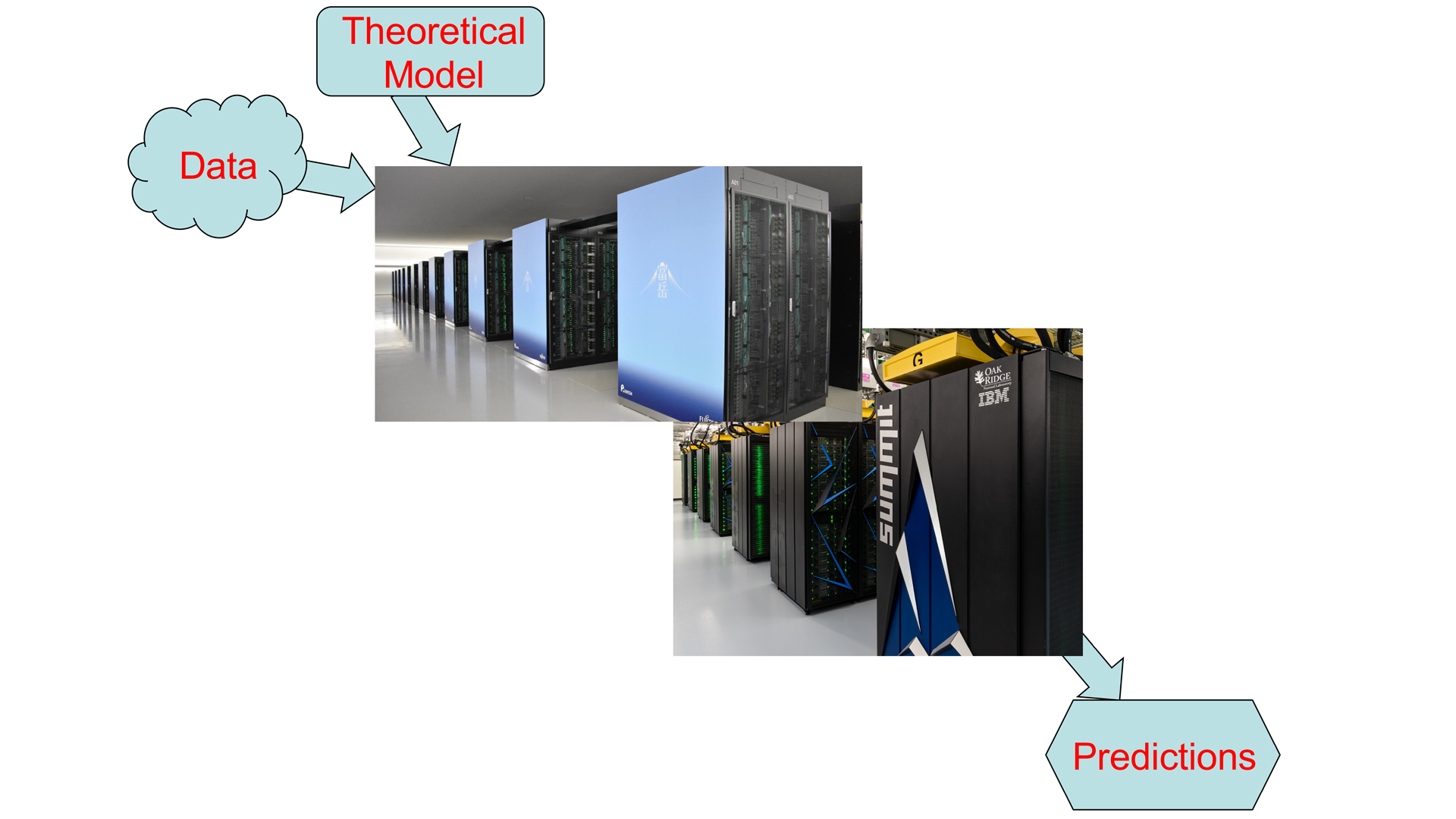
Do you ever wonder how your local weather is forecast for up to a week ahead of time? Well, it takes a combination of a highly tuned theoretical model that starts with the current weather and follows its time evolution on a supercomputer using all the relevant laws of nature. This “simulation” providing your weather forecast is an example of how supercomputers are revolutionising all areas of science and technology from elementary particles to how the Universe evolved from the Big Bang to the present time.
While the laws of nature, such as E = mc2, can appear to be deceptively simple, their application to complex systems on a supercomputer, such as the weather or the atomic nucleus, involves careful accounting for a multitude of detailed interactions among the many constituents where energy transfers occur. Here, a common theme emerges: to have accurate predictions for these complex systems, we need to follow the detailed consequences of the governing laws from the smaller to the larger space-time scales which can only be accomplished on a supercomputer (see Fig. 1).
Anomalous half-life of Carbon-14
To better appreciate the value of supercomputer simulations for basic science, we can take the example of the properties of the atomic nucleus. To be more specific, we can look at Carbon-14 which is well-known for its usefulness in archaeological dating due to its half-life of 5,730 years. Carbon-14 is produced in our atmosphere by cosmic rays resulting in a stable supply. Once something finishes its growth or is made, its Carbon-14, with eight neutrons and six protons, begins to decay away slowly over time by converting to Nitrogen-14, with seven neutrons and seven protons (see Fig. 2). Measuring the depleted amount of Carbon-14 in a sample tells how long it has been since the object was made. How does this transmutation occur and why does it take so long?
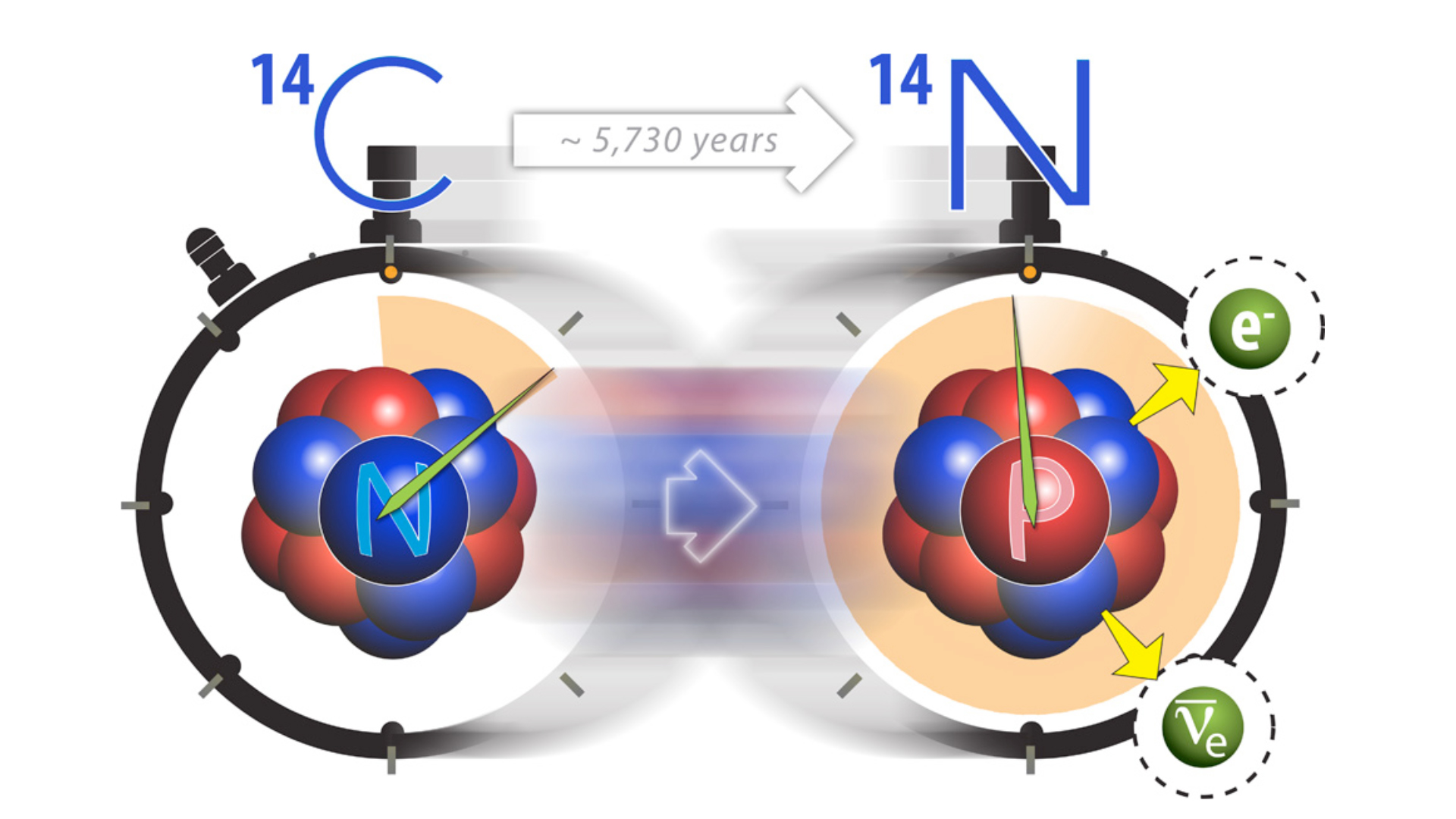
Herein was a long-standing problem. While we understood the basic laws governing the spontaneous transition of a neutron to a proton plus an electron and an antineutrino (beta decay) and we knew that a neutron outside of a nucleus undergoes this transition with a half-life of about 11 minutes (part of the “Data” in Fig. 1), we had not understood why this process takes 270 million times longer inside Carbon-14 despite many decades of careful research. It took a team of multi-disciplinary scientists and the world’s largest supercomputer in 2010, Jaguar at Oak Ridge National Laboratory, working together to solve this problem. Using more than 30 million processor hours on Jaguar they made a surprising discovery that the relevant laws of nature required a major improvement. The improvement states that 3 particles interacting simultaneously inside Carbon-14 do not behave according to the sum of their pairwise interactions. Instead, an additional 3-particle force is needed which plays a critical role in greatly slowing down the decay process [1].
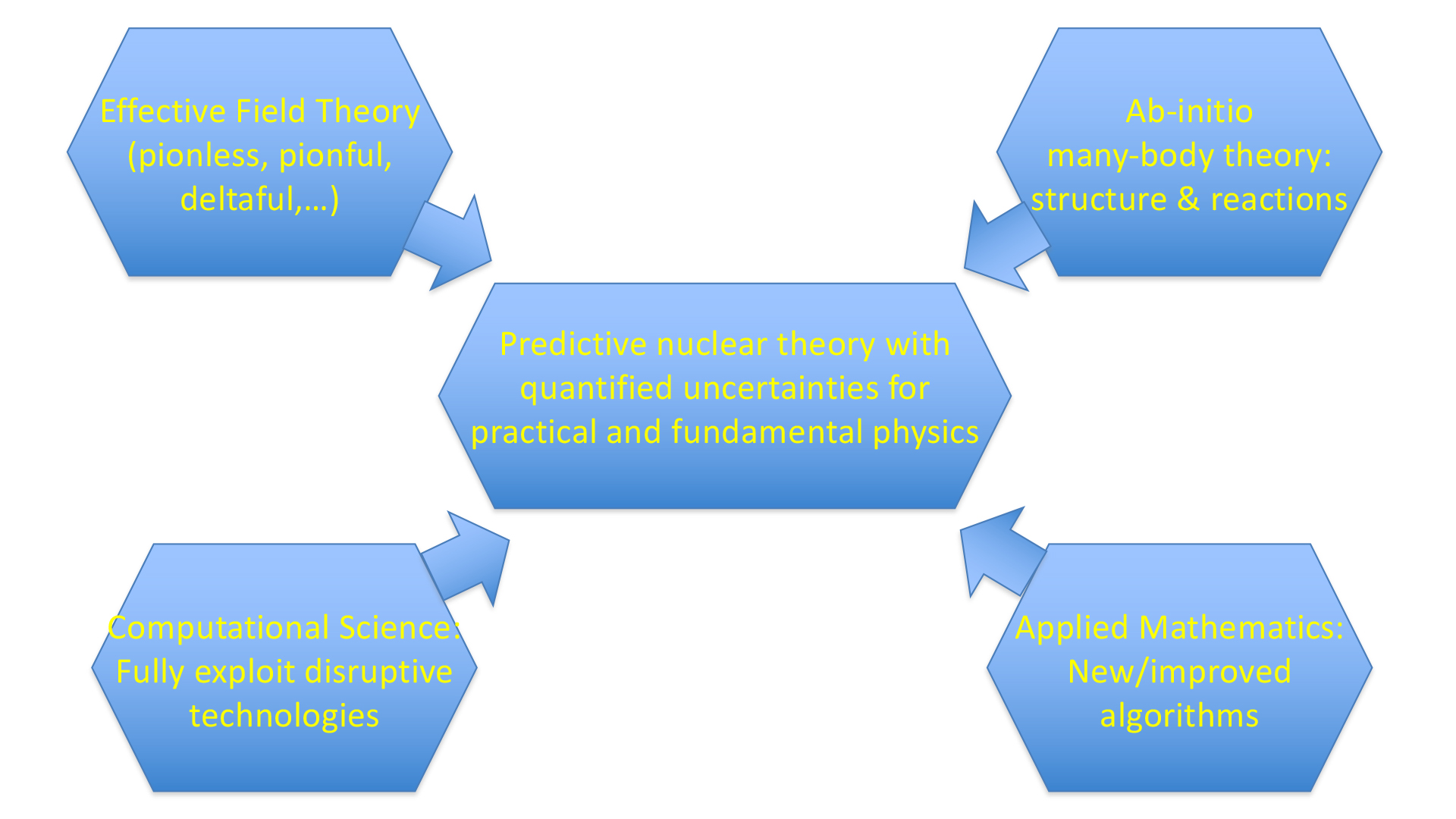
Let us consider the scientific ecosystem that enabled that discovery since it serves as an example of similar scientist/supercomputer ecosystems in science and technology today. Due to the complexity of the scientific issues and of state-of-the-art supercomputers, experts from diverse disciplines form teams to achieve a common scientific goal. The particular ecosystem that solved the 14 C half-life puzzle is emblematic of efforts to achieve reliable theoretical physics predictions. The measure of reliability is characterised by uncertainty quantification. Referring to the schematic in Fig. 3, these efforts involve partnerships of diverse theoretical physicists (upper two hexagons) working closely with computer scientists and applied mathematicians (lower two hexagons) in order to simulate the theoretical laws of nature successfully on current supercomputers.
Before we discuss what drives the need for supercomputers for solving these problems, let us consider what it takes to qualify as a supercomputer. This qualification changes frequently as newer, bigger and faster supercomputers are designed, built and delivered to the private and the public sector. Every six months, the world’s “Top 500” supercomputers are ranked by their performance on an array of standardised computational tasks. Today’s number one is Fugaku in Japan and number two is Summit in the United States (both pictured in Fig. 1). The United States also hosts four more of the world’s top 10 while China hosts two and Germany and Italy each host one.
Fugaku attained a whopping 442 x 1015 floating point operations per second (FLOPs) where multiplying two seven-digit numbers counts as one FLOP. The challenge for the multi-disciplinary team is to solve for the consequences of the laws of nature using all of Fugaku’s 7.6 million computer processing units (cores) working harmoniously and efficiently towards the simulation goal. To put this in perspective, simulating the entire earth’s weather would imply that each of Fugaku’s cores is responsible for a 26 square mile area – two and a half times the land area of Washington, D.C.
However, each of these zones is actually a 3-dimensional volume which is coupled to the simulations being conducted in its four neighbouring volumes. Hence, for each time step in the simulation all zones need to harmonise their results at their respective boundaries with their neighbours. Imagine the communication traffic at each time step! Also imagine the laws governing the time evolution taking energy inputs, outputs, and conversions into account on a sufficiently small spatial scale involving bodies of water and local geography to minimise the quantified uncertainties.
We now return to the question of what drives the need for a supercomputer. While understanding how to predict the weather (or the climate) on a supercomputer may seem intuitively obvious, the goal to simulate properties of an atomic nucleus brings in additional layers of complexity that challenge our common intuition. At the heart of the predictions are the laws of quantum mechanics that all eight neutrons and six protons in Carbon-14 obey simultaneously. The momentum and position of any single particle is not fixed in time but is represented as a distribution over space and how the energy flows among all the constituents is governed by an overall energy conservation law, by their inter-particle forces and by the “Pauli exclusion principle” (two identical particles cannot occupy the same state at the same time). According to the laws of quantum mechanics, we need to solve 50-million coupled second-order differential equations to obtain the properties of the Carbon-14 nucleus. Expressed in another mathematical way, we need to solve for the eigenvalues and eigenvectors of approximately a billion-by-billion dimensional matrix.
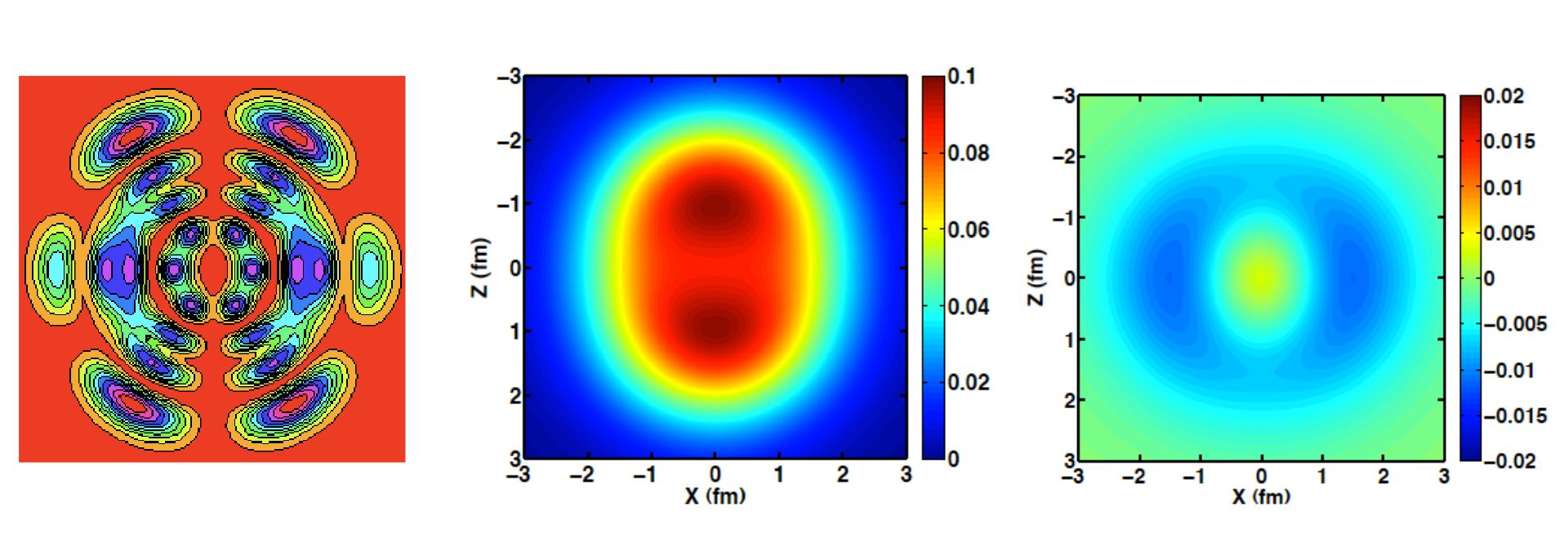
In order to help visualise the quantum mechanics, each of the particles in the nucleus spends part of its time in an orbit such as the one depicted in Fig. 4 (left panel). This is actually a density plot of a slice through the horizontal plane (y=0) of the orbit. To sense the entire orbit, imagine rotating it around its vertical axis in the plane of the page to obtain the full 3D density. According to the wave nature of particles in quantum mechanics, that particle is distributed over 3D space with that density distribution when it occupies that state. While that particle is in that state, the other particles are in other states represented by different 3D plots. All of these particles are constantly interacting with each other and each is bouncing around through hundreds of available states.
To promote our intuition, we can average the full quantum mechanical solution over time and average over the particles to produce a 3D density plot of the entire nucleus. The central panel of Figure 4 shows the resulting total density distribution for Beryllium-9 (again as a y=0 slice through the 3D plot) where two dense regions are visible, one above the other [2-4]. These dense regions represent two alpha-particles (two neutrons and two protons) separated by a gap. This indicates that clustering has emerged from the full quantum mechanical solution.
We can go further into the details. For example, since Beryllium-9 consists of four protons and five neutrons, we can subtract the proton from the neutron density to obtain the density of the odd neutron. Here we find an amazing feature: the odd neutron forms a donut-shaped ring, a torus, situated neatly between the two alpha particles, providing the effective bond between them. The right panel of Fig. 4 presents the y=0 slice through the odd neutron’s 3D distribution revealing the cross section of a torus.
Future of computational nuclear theory
Solving for the properties of many-particle quantum systems, such as atomic nuclei, is well-recognised as “computationally hard” and is not readily programmed for supercomputers. Valiant efforts of physicists, applied mathematicians and computer scientists (see Fig. 3), have led to new algorithms enabling solutions for the properties of the atomic nuclei with up to about 20 particles on today’s supercomputers [5-8]. However, this is only a small portion of nuclei and we need detailed understanding of many important phenomena occurring in heavier systems, such as astrophysical processes and fission. Hence, we will need new theoretical breakthroughs and increased computer capabilities to overcome current limits.
Owing to this need and similar pressures from other areas of science and technology to increase computational capacity as well as to the need to reduce electrical energy consumption, supercomputer architectures are evolving dramatically. Major changes now involve, for example, the integration of powerful graphics processor units (GPUs) and the adoption of complex memory hierarchies. In turn, these changes produce a need to develop and implement new algorithms that efficiently utilise these advanced hardware capabilities. What was “hard” before now becomes “harder” but, at the same time, more worthwhile since success in overcoming these challenges will enable new predictions and new discoveries.
What else does the future of supercomputer simulations hold? Here, two major paradigm shifts are already underway but will take from a few years to decades to reach full potential. The first is Machine Learning, a branch of Artificial Intelligence that is already proving to be a very powerful research tool that can effectively extend the capacity of supercomputer simulations by “learning” how their predictions depend on the size of the simulation and predict results for future simulations on the larger supercomputers of the future. The second major paradigm shift is the rapid development of quantum computing technology. Preliminary studies suggest that quantum computers will be capable of solving forefront unsolved problems in quantum mechanics such as the structure of atomic nuclei well beyond the light nuclei addressable with today’s supercomputers.
The promise of future scientific discoveries using these rapidly evolving computational tools, motivates a strong and balanced approach that fosters multi-disciplinary scientific endeavours such as those already proven successful.
Acknowledgment
The author acknowledges support from US Department of Energy grants DE-FG02-87ER40371 and DE-SC0018223.
References
[1] Pieter Maris, James P. Vary, Petr Navratil, W. Erich Ormand, Hai Ah Nam, David J. Dean, “Origin of the anomalous long lifetime of 14C,” Phys. Rev. Lett. 106, 202502 (2011).
[2] Robert Chase Cockrell, “Ab Initio Nuclear Structure Calculations for Light Nuclei,” (2012). Graduate Theses and Dissertations. 12654.
[3] P. Maris, “Ab Initio Nuclear Structure Calculations of Light Nuclei,” J. Phys.: Conf. Ser. 402, 012031 (2012).
[4] Pieter Maris and James P. Vary, “Ab initio Nuclear Structure Calculations of p-Shell Nuclei with JISP16,” Int. J. Mod. Phys. E 22, 1330016 (2013).
[5] Philip Sternberg, Esmond G. Ng, Chao Yang, Pieter Maris, James P. Vary, Masha Sosonkina, and Hung Viet Le. “Accelerating configuration interaction calculations for nuclear structure.” In Proceedings of the 2008 ACM/IEEE Conference on Supercomputing, SC ’08. IEEE Press, 2008.
[6] James P. Vary, Pieter Maris, Esmond Ng, Chao Yang, and Masha Sosonkina. “Ab initio nuclear structure: The Large sparse matrix eigenvalue problem.” J. Phys. Conf. Ser.,180:012083, 2009.
[7] Pieter Maris, Masha Sosonkina, James P. Vary, Esmond Ng, and Chao Yang. “Scaling of ab-initio nuclear physics calculations on multicore computer architectures.” Procedia Computer Science, 1(1):97–106, 2010. ICCS 2010.
[8] Hasan Metin Aktulga, Chao Yang, Esmond G. Ng, Pieter Maris, and James P. Vary. “Topology-aware mappings for large-scale eigenvalue problems.” In Christos Kaklamanis, Theodore Papatheodorou, and Paul G. Spirakis, editors, Euro-Par 2012 Parallel Processing, pages 830–842, Berlin, Heidelberg, 2012. Springer Berlin Heidelberg.








