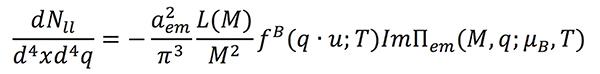Tetyana Galatyuk asks what can we learn from electromagnetic radiation about the state of visible matter under extreme conditions?
One of the great challenges in modern physics is to understand the evolution of our Universe from the ‘Big Bang’ to the state we observe today. Of particular interest is to unravel the microscopic properties of the extreme states of strong-interaction matter that existed, on the one hand, almost 14 billion years ago in the early Universe and, on the other, is created when two neutron stars merge, as recently observed for the first time. The possibility to form and explore in the laboratory strong-interaction matter under conditions similar to those realised a few microseconds after the ‘Big Bang’, or to those in the interior of compact stellar objects, is truly fascinating. The physics of those extreme states of matter is of pivotal significance for understanding a fundamental aspect of nature.
For most of human history, light was the only known part of the electromagnetic spectrum. Today, we know that visible light is just a small part of the electromagnetic spectrum and with dedicated detectors we can observe light over a large range of wavelengths.
The photon spectrum of the Milky Way, spanning over 15 orders of magnitude in wavelength, bears witness to this fact. The capability to detect electromagnetic radiation for such a large range in wavelengths is key to the enormous progress in astronomy and astrophysics. Indeed, the first detection of gravitational waves from a binary neutron star coalescence candidate (later designated GW170817) 1 and the observation of electromagnetic radiation from the same event 2 opened a new era in multi-messenger astronomy. The violent Universe can now be ‘heard’ through gravitational waves and ‘seen’ through electromagnetic radiation.
What can laboratory experiments tell us about extreme environments in the Universe?
Photons, the carriers of the electromagnetic force, have long been an essential tool to study the properties of ‘matter’. An illustrative example is the success story of mysterious electromagnetic radiation discovered by Wilhelm Conrad Roentgen, so-called ‘X-rays’. Since 1895, X-rays have allowed us to look through the human body. In 1900, Max Planck successfully described the thermal electromagnetic radiation emitted by a black body by introducing a quantisation concept.
Albert Einstein’s quantum theory of light proposed that light is composed of small packets of energy called photons that have wave-like properties. As one consequence, it was understood that the concept of photons could be generalised.
As mediators of a force, virtual photons can carry any combination of energy and momentum but have to materialise after a short time by the formation of a pair of charged leptons, e.g. an electron and a positron. Such virtual photons can serve as ideal probes of matter under extreme conditions of temperature (> 1012 K) and density (>280 Mt/cm3) in analogy to the role X-rays played. The theory of the strong force, Quantum Chromodynamics (QCD), predicts that under such extreme conditions ordinary matter (protons and neutrons) breaks into elementary building blocks, quarks and gluons.
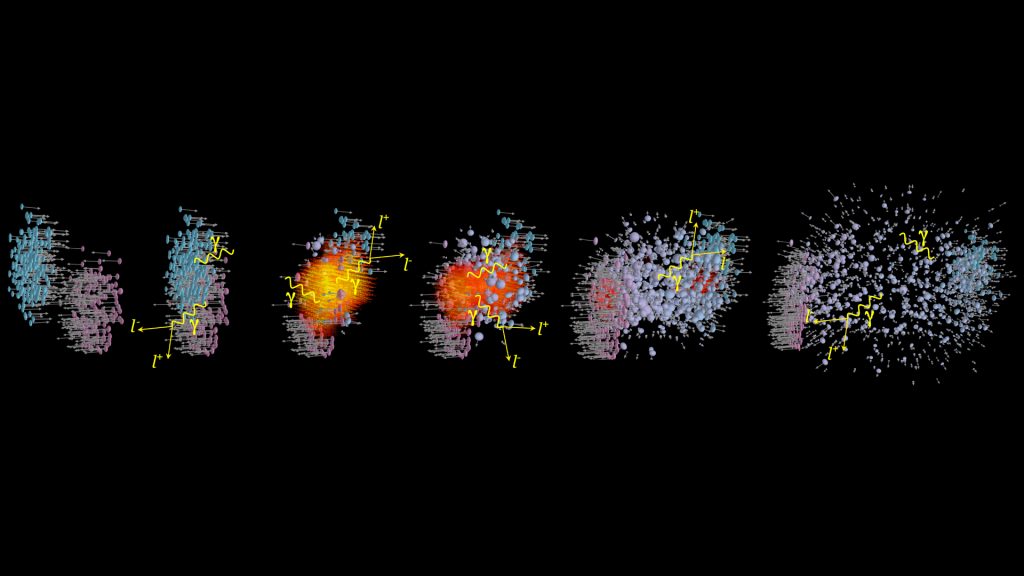
To recreate such extreme states of matter in the laboratory, one collides heavy nuclei accelerated to more than 90% of the speed of light. For an extremely short period of time, of order 10-23 seconds, transient states of QCD matter are produced in such collisions. Throughout the course of a heavy-ion collision, virtual photons are emitted (see Fig. 1) and offers a unique opportunity to directly obtain ‘Roentgen images’ of the hot and dense matter (in-medium electromagnetic spectral functions) and to measure its temperature by analysing ‘Planck-like’ spectral distributions.
Electromagnetic probes of strongly interacting matter
The electromagnetic (EM) interaction provides powerful tools for identifying and characterising conjectured novel phases of strong-interaction matter. Thermal emission of dileptons (e+ e– or μ+ μ–) and photons from the locally thermalised medium occurs throughout the lifetime of the fireball. Unlike hadrons, leptons do not interact strongly, leading to large mean free paths in the medium, much larger than the spatial extent of the fireball created in a heavy-ion collision. Hence, dileptons carry important information about the entire space-time history of the collision. Dilepton invariant-mass spectra are the only observable which gives direct access to the in-medium modification of hadronic spectral functions. This is evident from the 8-fold differential thermal production rate:3, 4
which depends only on the in-medium electromagnetic spectral function, ImΠem (the imaginary part of the current-current correlation function), its thermal weight in terms of the Bose-Einstein distribution, fB (q·u;T), and a free virtual-photon propagator, 1/M2.
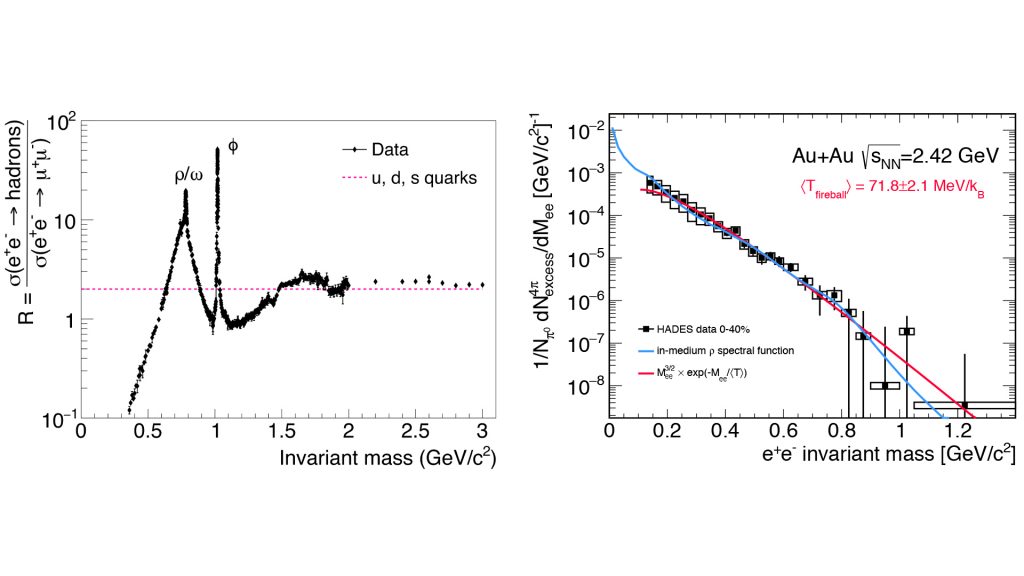
In the vacuum, ImΠem is accurately known from the inverse process of e+ e– annihilation into hadrons.5 As shown in Fig. 2 (left) it is characterised by two regions. At low masses (LMR), M<1.1 GeV/c2 its strength is concentrated in the light vector-mesons (ρ, ω, ϕ [7]); the non-perturbative phenomena of mass generation and quark confinement manifest themselves in massive hadronic degrees of freedom.
At masses M>1.5 GeV/c2 (IMR), the spectral function is in the perturbative regime, giving rise to a structure-less continuum of a weakly interacting quarks and anti-quarks (which subsequently fragment into multiple hadrons). The ρ-meson has received most of the attention in this context as it has a dominant contribution to the low-mass EM correlators and outshines the ω-meson by a factor of about 10.
Dileptons as spectrometer, thermometer, chronometer, barometer, polarimeter, and amperemeter of the fireball
The question is: how does the spectral function of the ρ-meson change inside hot and dense nuclear matter and which fundamental questions can be addressed with comprehensive measurements of dilepton production in heavy-ion collisions?
State-of-the-art measurements of dilepton ‘excess spectra’ (radiation from yellow-orange-red zone shown in Fig. 1) in nuclear collision from few GeV to few TeV energy and model predictions of thermal radiation from the QGP and hadronic phase that describe dilepton data available to date, show that the ρ meson undergoes a strong broadening in dense hadronic matter, melting into a continuous emission spectrum that resembles quark-antiquark annihilation.11 An example of dielectron ‘excess spectrum’ from baryon-dominated matter measured by the High Acceptance DiElectron Spectrometer (HADES) and theoretical analysis is shown in Fig. 2 (right).
Model calculations predict that depending on the invariant mass (M) and 3-momentum (q) of the dilepton ‘excess spectrum’ we can:
- Investigate the mechanism of chiral symmetry restoration in QCD matter12 and the transition from hadronic to partonic degrees of freedom11 through precise measurements of the dilepton invariant mass distributions in the LMR – dileptons as spectrometer. In between the LMR and IMR, for
M = 1.1-1.5 GeV/c2, the vacuum EM spectral function features a minimum structure, which is expected to be filled up by the so-called chiral-mixing effect as an additional signal of chiral symmetry restoration;13 - Measure directly the average temperature of the QCD medium emitting the continuum radiation. The invariant mass is not subject to a blue shift due to the collective expansion of the system – dileptons as thermometer;8, 6, 10
- The total thermal yields of low-mass dileptons can serve as a measurement of the total lifetime of the interacting medium – dileptons at chronometer;8, 9
- The (transverse) momentum distribution and azimuthal anisotropy is sensitive to collective expansion and by selecting different invariant mass regions contributions from early and late emission can be disentangled. This gives access to the evolution of collectivity – dileptons as barometer;14, 15
- Dileptons can also be used as a polarimeter, since the dilepton azimuthal anisotropy provides a promising observable to diagnose the mechanisms leading to emission of dileptons.16
- Another important application of dileptons is to use them to deduce transport coefficients. The electrical conductivity,17, 18, can be directly obtained as the low-energy limit of the electromagnetic spectral function and may be accessible through very soft dileptons, with masses and momenta below ~100 MeV/c2 – dileptons as amperemeter.
Dileptons and the QCD phase structures
A quantitative picture of the phase diagram of strongly interacting matter as a function of temperature and baryochemical potential has been discussed in details in [Stroth]. QCD inspired effective field theories, predict a rich structure of the QCD phase diagram, such as a first order phase transition between hadronic and partonic matter which terminates in a second order critical point (CP), or exotic phases like quarkyonic matter. The experimental approach is to probe with highest precision different regions of the QCD matter phase diagram.
The existing data from LHC, RHIC-BES, SPS, AGS, SIS18 allow accurate statements about the bulk properties of the matter created in heavy-ion collisions to be made. However, the challenge remains to locate the onset of QGP, to detect the CP and to study matter properties by isolating their unambiguous signals. The systematic and complete measurement at utmost precision of rare diagnostic probes not accessible so far in the high baryochemical potential region indicates a large discovery potential.
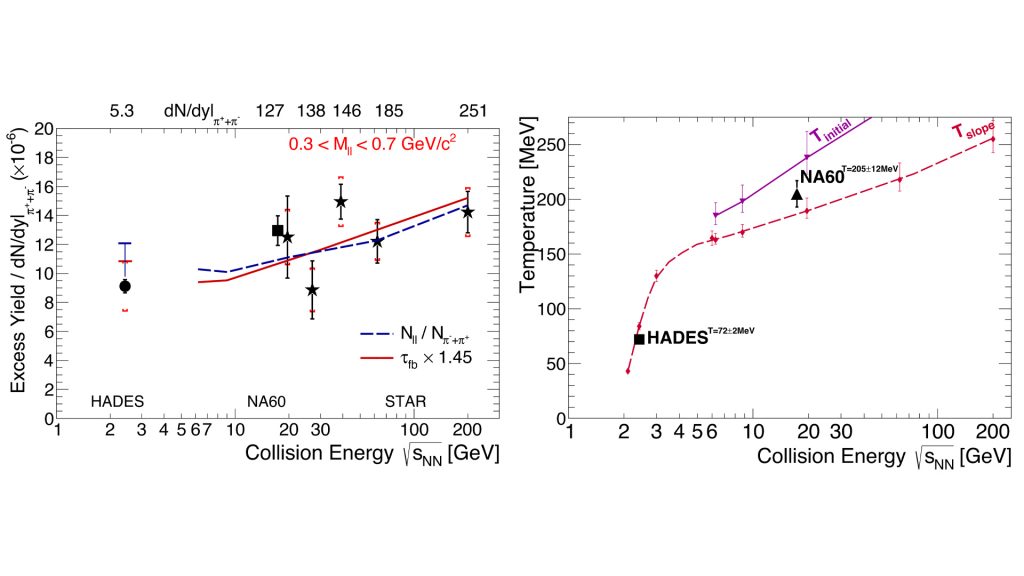
Various model calculations predict that the expansion of the compressed matter is slowed down when the system crosses a first-order phase transition. Large density fluctuations may lead to an enhancement of the dilepton yield. It has been demonstrated that the dilepton yield in the low-mass region could increase by factor of two-to-three in case of a first-order phase transition.19 Such an increase will be clearly visible in the otherwise rather smooth excitation function of the dilepton yield shown in the Fig. 3 (left). The measurement of an excitation function of the dilepton ‘excess spectrum’ shown in Fig. 3 (right) slope parameter covering collision energies from 2.4-10 GeV provides an excellent opportunity to trace the onset of QGP formation in nuclear collisions.
The average fireball temperature is systematically extracted from fits to the dilepton mass in the LMR and IMR assuming a Planck-like black-body radiation. A step in the caloric curve would indicate a first-order phase transition. Note that for both excitation functions, beyond the HADES measurements which currently go up to ~2.5 GeV for heavy ions, there are no dilepton/photon measurements in 2-8 GeV range available yet.
Extensive upgrade programmes at RHIC and the LHC will scrutinize the conditions of matter at small baryon chemical potential, which most closely resemble the early Universe. For low energies on the other hand, dilepton programmes are planned in Europe (FAIR, NICA, SPS) and Asia (J-PARC), which are aimed at study of the QCD phase diagram at high baryon densities, and, hence, of the interior of compact stellar objects. For example, the existence first-order phase transition might have significant implications for neutron star mergers and may be observable in the gravitational-wave spectrum produced in these merger events.
Dilepton experiments will thus continue to play a key role in the future the study of QCD matter in heavy ion collisions. The important prerequisite for success is the combination of high intensity beams and multi-purpose detectors with large acceptance, high efficiency, free streaming read-out electronics with high bandwidth online event selection.
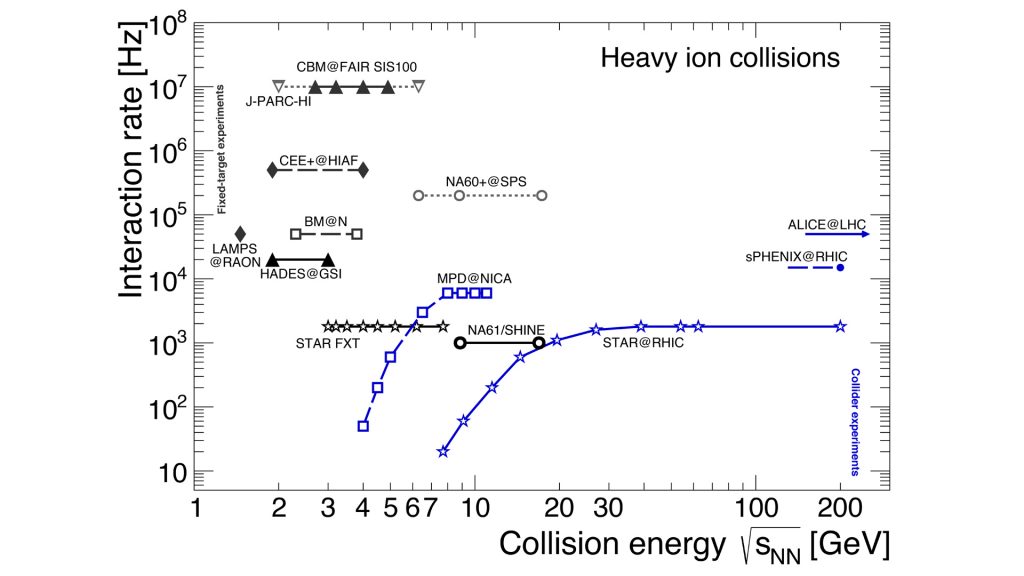
The new accelerator facilities are designed to have ever increasing luminosities. The rate capabilities of existing and planned heavy-ion experiments are presented in Fig. 4. The complete QCD phase diagram scan requires mutual collaborations extending out of nuclear physics into, high-energy particle physics, assisted by condensed-matter physics but in particular astrophysics and gravity. This is truly an interdisciplinary research area and new ideas are always desired.
References
1 B. P. Abbott et al., Phys. Rev. Lett., 119(16):161101, 2017
2 B. P. Abbott et al., Astrophys. J. Lett., 848(2):L12, 2017
3 R. D. Pisarski, Phys.Lett. B, 110:155–158, 1982
4 L. D. McLerran and T. Toimela, Phys. Rev. D,31:545, 1985
5 J. Beringer et al., Phys. Rev. D, 86:010001, 2012
6 J. Adamczewski-Musch et al., Nature Phys., 15(10):1040–1045, 2019
7 J. J. Sakurai, Annals Phys., 11:1–48, 1960
8 R. Rapp and H. v. Hees, Phys. Lett., B753:586–590, 2016
9 T. Galatyuk et al., Eur. Phys. J. A, 52(5):131, 2016
10 H. J. Specht, AIP Conf. Proc., 1322(1):1–10, 2010
11 R. Rapp and J. Wambach, Eur. Phys. J. A, 6:415–420, 1999
12 P. M. Hohler and R. Rapp, Phys. Lett. B, 731:103–109, 2014
13 M. Dey, V. L. Eletsky, and B. L. Ioffe, Phys. Lett. B, 252:620–624, 1990
14 R. Arnaldi et al., Phys. Rev. Lett., 100:022302, 2008
15 D. Dittert, Ukr. J. Phys., 64(7):560–565, 2019
16 E. Speranza, A. Jaiswal and B. Friman, Phys. Lett. B, 782:395–400, 2018
17 H.-T. Ding et al., Phys.Rev. D, 83:034504, 2011
18 J. Atchison and R. Rapp, J. Phys.Conf. Ser., 832(1):012057, 2017
19 F. Seck et al., e-Print: 2010.04614 [nucl-th]
20 T. Galatyuk, Nucl. Phys. A,982:163–169, 2019
Please note, this article will also appear in the eighth edition of our quarterly publication.