Exploring matter 10 microseconds after the Big Bang

Professor John W Harris, from Yale University’s Department of Physics, discusses how a better understanding of what happened immediately after the Big Bang could enable breakthroughs in our understanding of quantum chromodynamics.

Within just 10 microseconds after the Big Bang, the Universe had expanded and cooled from its conception at the Planck temperature¹ (~10³² Kelvin) to a ‘mere’ temperature of ~2×10¹² Kelvin, still 200,000 times hotter than our Sun today. At that time, matter in the universe was in the form of a hot soup of quarks and gluons, called the quark-gluon plasma (QGP).

As the Universe cooled further, the matter experienced a phase transition from this hot liquid soup into cooler individual particles, akin to water freezing to ice crystals when it cools. Today, under much cooler conditions in the Universe, quarks and gluons are found to be the primary constituents of nuclear particles, for example inside the protons and neutrons that form the nucleus at the centre of atoms.

Replicating conditions after the Big Bang

Scientists have been able to create the QGP in the laboratory on Earth through the use of very large accelerators which collide atomic nuclei at near the speed of light (c). These nuclei range in mass from the lightest nucleus (hydrogen) to the very heavy (such as uranium). When the nuclei collide, their oppositely-directed relative motion compresses the collision region where they overlap, creating matter at extremely high densities to form the QGP. The relative kinetic energy of the incoming nuclei is also then transformed into creating matter. This is in accordance with the famous formula E=mc², which says that the energy (E) and mass (m) of matter are interchangeable properties, related by the speed of light (c).

In creating matter from energy in these high energy collisions, equal amounts of matter and anti-matter are formed in order to obey conservation laws in physics. In a near head-on collision at the higher energies at the LHC, tens of thousands of particles and antimatter particles are created² from the energy in a single collision. The QGP then cools and expands to a temperature ~ 2×1012 Kelvin, as in the early Universe 10 microseconds after the Big Bang, a ‘friendlier temperature’ allowing for the formation of subatomic particles and anti-particles after cooling. The particles emerge from the collision to be detected in the large detectors at the RHIC and LHC colliders.

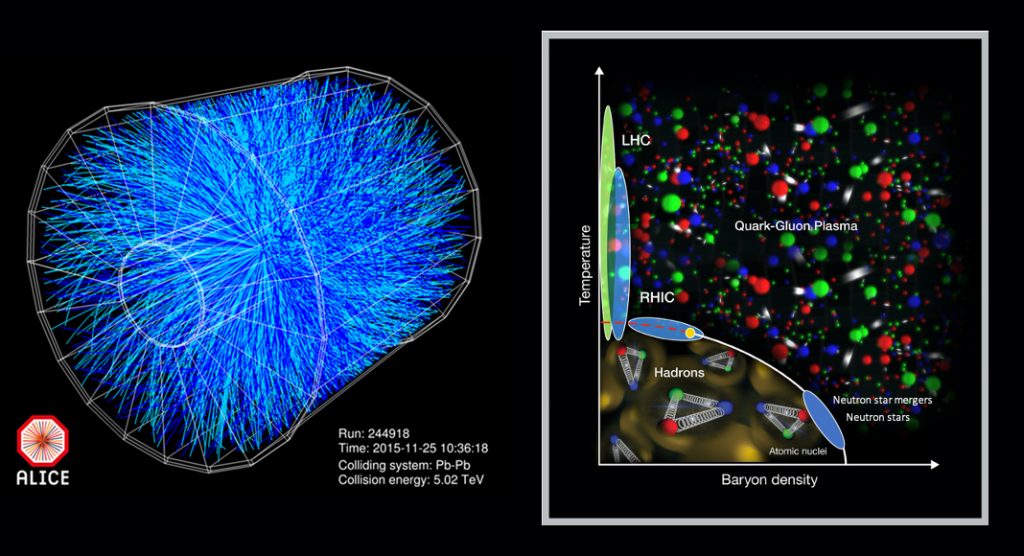
The overall goal of this investigation is to understand the phase diagram of Quantum Chromo-Dynamics (QCD), the theory of the strong interaction that governs interactions in particle and nuclear physics aside from the weak interactions. Shown in Fig. 1 is the phase diagram for QCD matter. The phase diagram represents the landscape for the various types of matter in QCD as a function of temperature and baryon³ density. Atomic nuclei are indicated at low temperature and intermediate density in the diagram. They consist of protons and neutrons, which each have three quarks as depicted by the colour-neutral red-green-blue triangular configurations and held together by gluons (appearing as springs) that facilitate the strong interaction. Nuclei can be in excited states as illustrated by those located at higher temperature. Likewise, all subatomic particles, collectively known as hadrons,³ can exist at higher temperatures up to the white curve that indicates the location of the phase transition from subatomic particles to the interacting quarks and gluons that form the QGP. The yellow point at the end of the curve signifies a possible critical point in the phase transition, which is being investigated in a thorough beam energy scan programme at RHIC.⁴

Beyond the white curve at higher temperatures and/or baryon densities is the region of the QGP. At low temperatures and high baryon densities reside neutron stars and neutron star mergers that have been observed recently. At baryon densities beyond those of neutron stars, there are predictions of the possible existence of colour superconductivity of quark pairs, much like Cooper pairs which produce electrical superconductivity.

Techniques

The field has utilised techniques from a variety of disciplines to investigate properties of the QGP. Experimental techniques for the design and construction of detectors for large collider experiments have benefitted from advances in nuclear and particle physics, sometimes even utilising entire experiments themselves designed for other purposes, such as those for the Higgs discovery at the LHC. In order to reveal the size and dynamics of the interaction during and after formation of the QGP following the Big Bang, a special analysis technique originally developed to determine the size of stars was adopted from astronomy and astrophysics. This technique based upon the Hanbury Brown – Twiss Effect capitalises on the statistical mechanics of photons, pi-mesons, and other particles with integer values of spin.

Using intensity interferometry applied originally to stars, the QGP is found to have a size up to ~7×10^-15m and may exist for a few times 10^-23 seconds in heavy-ion collisions prior to evaporating into hadrons as it cools and expands at a fraction of light speed. All along it radiates photons, much like that of black-body radiation, from which an average temperature of the system approximately several times 10¹² Kelvin is found. Thermal and hydrodynamical models can be used to determine additional properties of the QGP. The temperature at the time that hadrons form, derived from the measured ratios of various types of particles and anti-particles and compared to calculations of their creation from a thermal system, is found to be approximately a few times 10¹² Kelvin. This is the temperature of the quark-hadron phase transition in the early Universe. From transport models and fluctuations of the collective flow in the QGP, properties such as the shear and bulk viscosities and the speed of sound in the medium can be derived.

Discoveries and properties

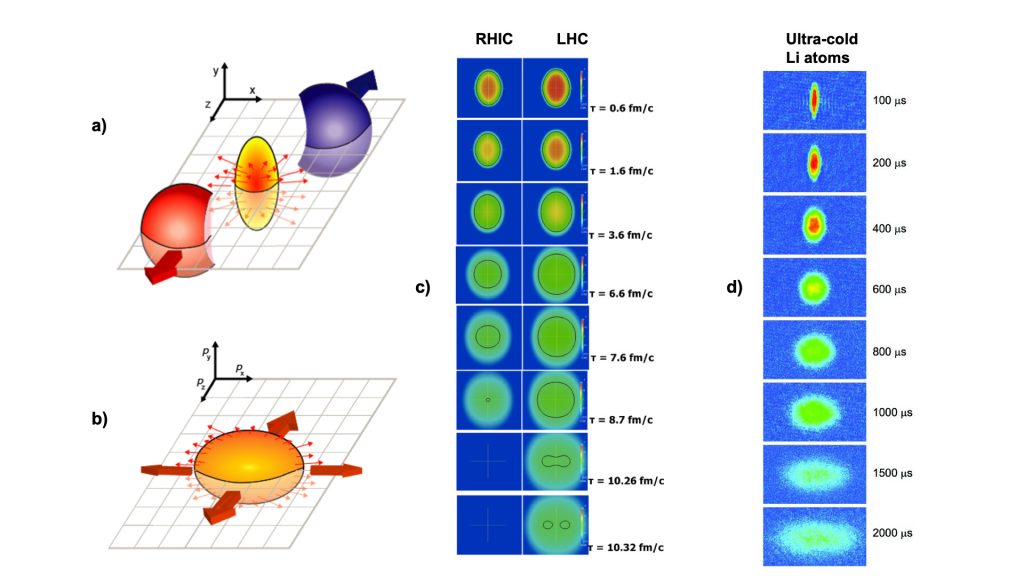
In order to gain some understanding of the evolution of these collisions, a few key experimental results along with their theoretical interpretations will be presented. An artist’s drawing of two nuclei colliding at relativistic (near light speed) velocities along the Z-axis is shown in Fig. 2a. The collision overlap region where the QGP is formed (in yellow) is asymmetric in the X-Y co-ordinate plane or elongated along the y direction. Fig. 2b is an illustration of measurements of the momenta of particles after the collision, which is found to be elongated along the X direction. The initial asymmetry in co-ordinate space transforms into a momentum space anisotropy perpendicular to the initial asymmetry of the collision. This is understood as a pressure difference in the compression in the initial overlap region during the collision that expands rapidly in the direction with the strongest pressure gradient along X, which is the shortest distance for decompression as depicted by the thin arrows. This has been described thoroughly by 3D hydrodynamics as formation of the QGP, then expansion and cooling, and finally particles flowing preferentially in the X-Z plane as shown in Fig. 2c.

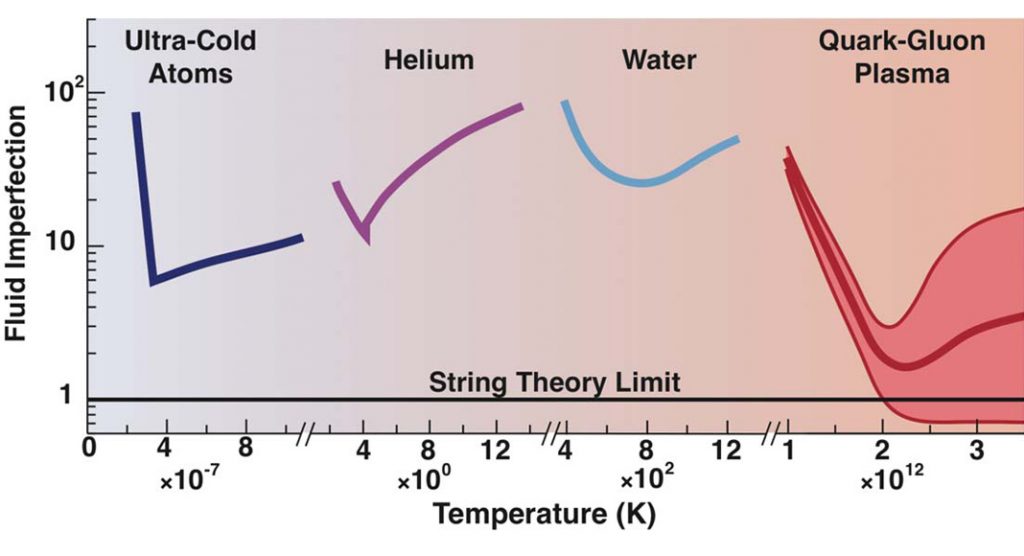
The theory invokes nearly ideal hydrodynamics of a strongly interacting system that flows collectively with extremely low sheer viscosity and near-perfect fluid behaviour. The behaviour of the QGP turns out to be analogous to that of a very different, strongly interacting system of ultra-cold atoms at a very low temperature (~10^-6 Kelvin). Fig. 2d is a time sequence of the expansion of ultra-cold atoms observed in experiment.⁶ Notice the similarity between expansion of the ultracold atoms and the QGP that is ~10¹⁸ times hotter. String Theory⁸ predicts a universal lower bound for the sheer viscosity to entropy ratio, which can be described as a resistance to flow, for strongly-coupled systems and depicted in Fig. 3. An intriguing aspect is that this lower limit is approached by each of these strongly-coupled systems even though they are at vastly different temperatures.

A long-standing prediction for the formation of a QGP is that it leads to an enhanced production of particles that contain strange quarks. The strange quark is the next more massive (heavier) quark after the light quarks that make up most subatomic particles, such as protons and neutrons in nuclei. Since the temperature of the QGP is high, particles with strange quarks and anti-quarks can be produced thermally at these high temperatures. Fig. 4 (left) presents results on the production of strange particles with one (K⁰, Λ), two (Ξ) and three (Ω) strange quarks relative to light quark particles (π) in p+p (proton+proton), p+Pb and Pb+Pb collisions as a function of the number of produced particles in the event at the LHC.⁹ The strangeness enhancement is observed to increase with the particle multiplicity and is most pronounced for the more massive nuclei (Pb+Pb) in the collision.

One surprise is that the strangeness enhancement appears also in the highest multiplicity p+p collisions, something never seen before. Does this indicate that a QGP is formed in the most violent p+p collisions that produce a tremendous number of particles and anti-particles? This is unexpected but may be the case since in high-multiplicity p+p events strangeness production reaches values similar to those observed in Pb+Pb collisions where a QGP is formed. This is an outstanding question that is under intensive current investigation: what is the smallest droplet of a QGP that can be formed and how might it be created?

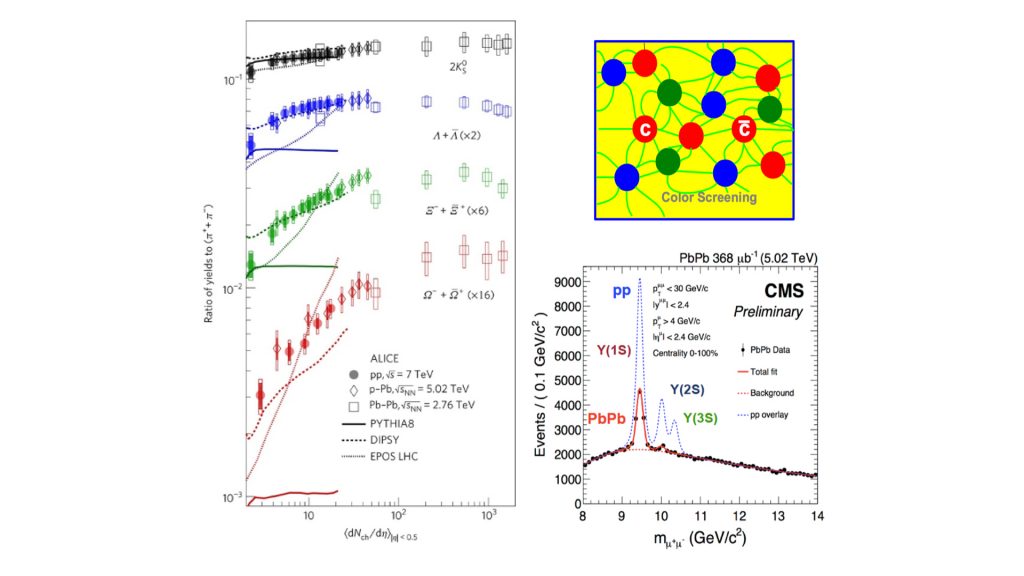
The next heavier quarks after the strange quark (s) are the charm (c) and bottom (b) quarks. The top right image in Fig. 4 is an artist’s conception of the production of a b quark and b anti-quark pair, which can combine to form a Υ bound state in the sea of light quarks that make up the QGP. The b quark and b anti-quark pair have their strongly-attractive mutual colour force screened by immersion in the QGP sea of light quarks. Thus, it is difficult to easily find another b quark of the opposite type (quark versus anti-quark) to form the Υ bound state, which is a b quark and b anti-quark pair.

The bottom right graph in Fig. 4 presents results on the production of the ground state Υ(1s) and the progressively higher-lying excited states Y(2s) and Υ(3s) in p+p (blue) and Pb+Pb (red) collisions. The three Y states are observed and appear as peaks in pp collisions, however the Υ(1s), Υ(2s), and Υ(3s) peaks in Pb+Pb collisions are progressively more suppressed relative to p+p collisions, with the Υ(3s) no longer visible. These measurements in Pb+Pb collisions support the concept of screening of the strong force, which binds the Υ states: the higher the excited state, the less tightly bound it is; and thus less likely to be formed, to survive in the QGP, and to appear as a peak in the data.

Strangeness enhancement, quarkonium suppression, and collective flow of a nearly perfect liquid all provide evidence for formation of a QGP. In addition to these, a phenomenon called ‘jet quenching’ is observed. A jet is a collimated stream of particles that results when a fast quark or gluon transforms into particles. Jet quenching and energetic particle suppression result in a reduction in the number of very energetic jets and particles due to their QCD interactions in the QGP. A conceptual diagram of a collision is presented in Fig. 5a with a very energetic particle or jet seen emerging from the QGP.

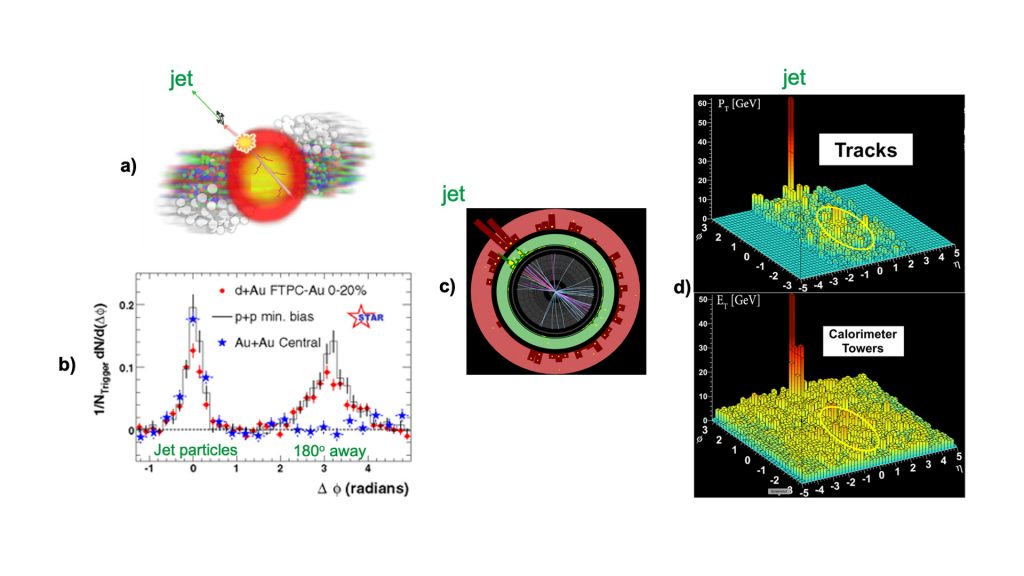
Energetic particles and jets originate from collisions of two incoming quarks and/or gluons in the heavy-ion interaction. Jet quenching has been observed for particles on the opposite side of a jet, where they are modified or disappear as seen by their absence on the side opposite the jet in Fig. 5a. This was first observed in the data in Fig. 5b at RHIC in near head-on collisions of Au+Au (blue symbols),¹¹ where jet particles peak at 0° along the jet direction, but are not observed 180° opposite the jet. The jet and particles on the opposite side are quenched, having lost energy through interacting in the hot QGP and do not escape. The QGP behaves as an opaque liquid, which is consistent with having a short mean-free path in a strongly-coupled system. In contrast, a peak is observed on the opposite side in collisions of the smaller systems, p+p (histogram) and d+Au (red), where no QGP is expected in these smaller systems at the lower energies of RHIC. Results from higher energy collisions at the LHC are shown in Fig. 5c in an end view and in Fig. 5d in a perspective of towers of a trigger jet and remnants of a highly quenched jet on the opposite side.

Connections to other fields of research

Understanding the properties of the QGP and the QCD phase diagram is of cross-disciplinary interest. This is now a dynamic field of investigation that has overlap and shared interest in novel physics being investigated in other fields. This has led to more generalised approaches in describing and understanding strongly-coupled systems. The strongly-coupled QGP has properties similar to those of ultra-cold atoms⁶ and strongly-correlated electron systems¹² in condensed matter physics, and more generally to strongly-coupled quantum matter.¹³ There has been an increasing number of applications of string theory to describe these strongly-coupled systems.^13,14,15 Holography in four dimensions is able to map a difficult problem in strongly-coupled quantum field theory into a tractable problem of classical gravity in five dimensions. This has led to predictions of dynamical properties of fluids such as that depicted in Fig. 3.

Theoretical research continues to strive to understand the dynamical evolution of strongly coupled matter under a variety of conditions such as those for QCD matter indicated in Fig. 1. This is a broad endeavour extending from the time before the early Universe cooled from the era of quarks to subatomic particles and light nuclei, to much later in the evolution of stars and neutron stars that may contain quark matter in their cores. There is new and potential future experimental evidence from gravitational wave observations in neutron star mergers to test theoretical calculations that predict the existence of quark matter during the neutron star merger process. Observations of future neutron star merger events in gravitational wave observatories such as LIGO and VIRGO may be able to identify signatures of quark matter formation in their signals during the merger process.

Summary overview and the future

The field of relativistic heavy-ion physics has reproduced in the laboratory conditions that existed in the very early Universe, directly after the Big Bang, when matter was in the form of quarks and gluons at extremely high temperature, called the quark-gluon plasma. The quarks and gluons at these temperatures are observed to flow readily with very little resistance to flow and approach a universal lower limit for the viscosity/entropy ratio of strongly-coupled systems. A few key measurements and concepts have been presented here to provide an understanding of the dynamical evolution of the collisions, the progress in understanding the properties of the QGP, and connections to related forefront physics in other fields.

There are still many questions about the QGP, some of which may be answered soon and could lead to breakthroughs in our understanding of QCD. Is there a critical point in the QCD Phase Diagram that is currently being investigated in the beam energy scan programme at RHIC, and what will be learned from those results? Whether and how theoretically could a QGP emerge from very violent collisions of small systems (proton+proton) and dynamically evolve into collisions of heavy nuclei as the energy density (temperature) is increased? In other words, what is the smallest droplet of QGP that can be formed and specifically what are the underlying mechanisms that lead to its formation? This question is rather complicated as it involves a deeper understanding of the underlying evolution of the dynamical mechanisms in the initial and final state of the collisions that contribute to its formation. Thorough understanding of the dynamical properties of quarks and gluons in the initial state of the incoming nuclei may have to wait, but will be pursued in research at the future Electron Ion Collider.

A continuing goal of the field is to determine more precisely through experiments the dynamical properties of the QGP. Through future experimental investigation and theoretical inquiry, properties of the QGP such as the speed of sound or sound attenuation length, its shear and bulk viscosities, Reynolds number, and the colour screening length of the strong interaction can be determined as a function of temperature of the system. This will involve the better statistical sensitivity with new and faster detector systems, which allow measurements of higher order moments and fluctuations of these properties in heavy-ion collisions to be achieved, accompanied by innovations in theoretical approaches and faster computers. Given the strong universal interest in the behaviour of strongly coupled systems, further measurements and advances in understanding the QGP and its properties will be an active area of research and broad interest for the foreseeable future.

Acknowledgements

This work was supported by the Office of Nuclear Physics in the Office of Science of the US Department of Energy.

References

1. The Planck temperature is the hottest temperature possible. An object at this temperature emits photons with wavelengths of a Planck length, which is the quantum of length, the smallest possible unit (~10^-35m) in quantum mechanics
2. Light anti-nuclei have also been discovered, see ‘Observation of the antimatter helium-4 nucleus’
3. Baryons are subatomic particles that contain three quarks, such as the protons and neutrons that make up the atomic nucleus. Mesons are subatomic particles that have one quark and an anti-quark. Baryons and mesons are subsets of particles called hadrons
4. STAR Collaboration, ‘An Experimental Exploration of the QCD Phase Diagram: The Search for the Critical Point and the Onset of De-confinement’, arXiv:1007.2613 [nucl-ex]
5. Shen et al. ‘Radial and elliptic flow in Pb + Pb collisions at energies available at the CERN Large Hadron Collider from viscous hydrodynamics,’ Phys. Rev. C 84 (2011) 044903
6. KM O’Hara et al. ‘Observation of a Strongly Interacting Degenerate Fermi Gas of Atoms,’ Science (2002) Volume 298, 2179.
7. Figure courtesy of S. Beckman and J. Nagle, https://science.osti.gov/-/media/np/nsac/pdf/20130201/2013_NSAC_Implementing_the_2007_Long_Range_Plan.pdf, adapted from Physics Today 58, 5, 23 (2005) and reference 8
8. K. Kovtun, D. T. Son, A. O. Starinets. ‘Viscosity in Strongly Interacting Quantum Field Theories from Black Hole Physics,’ Phys. Rev. Lett. 94, 111601 (2005)
9. ALICE Collaboration. ‘Enhanced production of multi-strange hadrons in high-multiplicity proton–proton collisions,’ Nature Physics Letters, 24 April 2017 https://doi.org/10.1038/nphys4111
10. Hu et al. ‘Review of bottomonium measurements from CMS’, Int. J. Mod. Phys. A 32 (2017) 1730015
11. STAR Collaboration, Physical Review Letters 90 (2003) 082302; ibid 91 (2003) 072304
12. Sachdev. ‘What Can Gauge-Gravity Duality Teach Us About Condensed Matter Physics?’ Annual Review of Condensed Matter Physics 3 (2012) 9–33 www.annualreviews.org/doi/abs/10.1146/annurev-conmatphys-020911-125141
13. Franz, M., Rozali. ‘Mimicking black hole event horizons in atomic and solid-state systems’, Nat Rev Mater 3, 491–501 (2018) https://doi.org/10.1038/s41578-018-0058-z
14. Maldacena. ‘The Illusion of Gravity’, Scientific American (November 2005) 57 https://www.scientificamerican.com/article/the-illusion-of-gravity
15. Hartnoll. ‘Stringing Together a Solid State,’ Science 322, 1639 (2008) https://science.sciencemag.org/content/322/5908/1639.full

Professor John W Harris
Department of Physics
Yale University
+1 203 432 6106
john.harris@yale.edu
Tweet @YalePhysicsDept
https://wlab.yale.edu
https://star.physics.yale.edu/johnharris