A team at the Triangle Universities Nuclear Laboratory (TUNL) is using the beam at the High Intensity Gamma-Ray Source (HIγS) to explore nucleon structure using Compton scattering.
The Big Bang theory, which represents our best understanding of the origin of the Universe, predicts the creation of all matter. According to this theory, as the Universe expanded and cooled, the fundamental forces became distinct, and the kinetic energies of the elementary particles decreased, setting the stage for the synthesis of nucleons (protons and neutrons). Being the predominant constituent of visible matter, the nucleons arise in the first one-millionth second of the Universe’s life as composite objects from the confinement of quarks, their fundamental constituents. This period was followed by an epoch of nucleosynthesis in which relatively lighter nuclei and elements were produced in the first few hundred seconds after the Big Bang.
Even though the Big Bang theory explains the physical cosmology successfully in great depth, the current quantitative understanding of the phenomena of nucleon formation is poor. The challenge lies in the treatment of strong interactions at large distance scales – or low energy – the scales at which the nucleons are formed. The theory that best describes these strong interactions is Quantum Chromodynamics (QCD). The standard technique in QCD calculations at high energies and short distances is to treat the strong interaction as a perturbative contribution. This approach succeeds because the strong coupling logarithmically decreases as the energy increases. However, at low energies and long distances a sharp increase in the strength of the coupling requires a non-perturbative approach.
Alternative approaches include Effective Field Theories (EFTs) and brute-force computation using lattice QCD. The lattice calculations are maturing fast and some observables similar to the ones computed in EFTs can be reproduced. The EFTs are built on the scaffolding of QCD symmetries, such as chirality, and hence the corresponding EFT (χEFT) and a chosen set of degrees of freedom. The beauty of the EFT technique lies in its traceable connection to QCD. The χEFTs have been experimentally tested at appropriate distance scales for many observables and have generally been in good agreement with measurements with good precision.
Observing the nucleus
Just as microscopes are used to observe objects too small for our eyes to discern, we need particle beams to probe the features of the nucleus and the nucleons inside it. A frequently used probe in the fields of biology, chemistry, and physics is light. We have been able to use light to study many types of objects and associated phenomena by adjusting the wavelength and frequency of the light to match the spatial dimensions and excitation energies of the system being probed.
We have been able to use light to study varying types of objects and associated phenomena due to the wavelength and frequency of light. In the visible part of the light spectrum, frequency is represented by colour. Longer wavelengths than visible light represent infrared, micro-, and radio-waves. Alternatively, shorter wavelengths than visible light are represented by ultraviolet, X-rays, and gamma-rays. It is only with the help of shorter wavelengths or gamma-rays that we are able to resolve features of nuclei and nucleons. At this extreme end of the spectrum, the wavelengths approach less than one-trillionth of a metre, a distance scale which matches the size of nuclei and nucleons.
Light is a suitable choice as a nuclear probe because light waves are in fact electric and magnetic fields oscillating in time. In the Standard Model of elementary particle physics, the electromagnetic (EM) force is the best understood fundamental interaction. As the EM-fields carry the quanta of the EM-force, their interactions with nuclei and nucleons are in-turn widely studied and well-understood.
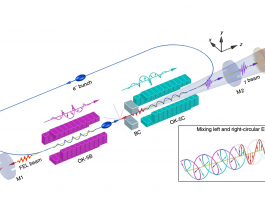
At the High Intensity Gamma Ray Source (HIγS), gamma rays are produced via the process of Compton backscattering of Free-Electron Laser (FEL) photons by high-energy electrons circulating in a storage ring. As shown in Fig. 1, HIγS is comprised of three major accelerator systems: a linac injector, a booster synchrotron, and a race-track shaped electron storage ring that contains a set of planar or helical undulators in one of the straight sections which constitute the FEL system.The stored electron bunches produce coherent radiation as they are agitated by the undulator electromagnets, this radiation is then trapped inside an optical cavity. The radiofrequency of the electron bunches (e-bunch) is adjusted such that the FEL photons produced by one e-bunch and travelling inside the optical cavity are backscattered by another e-bunch which has been phase-shifted by the length of the optical cavity. This process of Compton backscattering boosts the energy of the FEL photon from just a few electron-volts (eV) to millions of electron-volts (MeV), resulting in the production of gamma rays. The mirrors of the optical cavity are transparent to the gamma rays which are then transported to the target room for experiments.
We present here two studies using gamma rays which are the focus of understanding the nucleon structure and their interactions in the energy region and at distance scales where Low-Energy QCD and χEFTs are relevant.
Compton scattering
The first of these programmes studies the scattering kinematics of gamma rays from target nuclei, a phenomenon called Compton scattering in honor of Arthur Compton, who was awarded the Nobel Prize in Physics in 1927 for his discovery of this process by scattering X-rays from atomic electrons. In nuclear and nucleon Compton scattering, the polarised or unpolarised EM fields carried by the gamma rays induce a distortion of charges and currents associated with single or few interacting nucleons. For example, if you consider a nucleon as a classical object with charge and mass, then the applied electric field of the gamma rays will induce a distortion of charge and mass resulting in an induced dipole moment. The ratio of the induced dipole moment and the strength of the applied electric field is called the electric dipole polarisability aE. The electric polarisability encodes the tendency of the nucleon to be distorted, hence it is classified as one of the parameters which describe the internal structure of the nucleon. The same analogy can be applied to the relation between the magnetic fields and the currents, resulting in an induced magnetic dipole and magnetic polarisability βM.
In addition to the observables such as the electric and magnetic polarisabilities, Compton scattering can be used to extract other nucleon structure functions. One such set of observables are called spin-polarisabilities. Classically, spin-polarisabilities can be viewed as the nucleon equivalent of the Faraday effect. For example, the forward spin-polarisability, γ0, is indicated by the stiffness of the proton spin in response to coupling with the externally applied transverse electric and magnetic field components of the gamma rays. Alternatively, one can view this distortion of the proton spin as an interplay between the induced diamagnetic charged pion cloud currents and the paramagnetic excitation of the proton, known as the Δ-resonance. Measurement of the EM and spin-polarisabilities are crucial to validating the predictions of the χEFTs.
More broadly, in this theoretical framework the Compton scattering amplitude can be expanded in the powers of the incident gamma ray or photon energy (ω). The zeroth-order term is simply the resolution of the point charge (Q) and carries no information on the internal structure of the nucleon. The first order term contains the information on the anomalous magnetic moment (k) of the nucleon and can be accessed with helicity-dependent photo-absorption cross sections in the form of the Gerasimov-Drell-Hearn Sum Rule (GDH). The second-order term is the first so-called ‘structure term’ in the Compton scattering amplitude and contains the dependency on the electric and magnetic polarisabilities. The next order term O(ω3) contains a set of structure functions dependent on the spin-polarisabilities. The experimental programme at HIγS is committed to measuring the GDH sum rule for the deuteron, electric and magnetic polarisabilities of the proton and neutron, and the proton spin-polarisabilities. As an example of this broad programme, we will discuss the case of neutrons aE and βM.
The reason for focusing on the polarisabilities of the neutron is not arbitrary. The current status of the experimental measurement of EM polarisabilities is as follows: the proton aE is known to approximately 3% statistical uncertainty. The case of proton βM is slightly worse with statistical uncertainty of 11%. However, the case for the neutron is far worse. The neutron aE is only known to about 10% and βM to 34% statistical uncertainties, and these experimental and theoretical challenges arise due to the absence of free neutron targets. Therefore, the standard technique is to measure the iso-spin averaged nucleon polarisabilities from Compton scattering cross sections on light nuclei such as the deuteron (n+p) and 3He (2p+n), and then extract the neutron values by subtracting the better-known proton values.
The extraction of nucleon polarisabilities requires measurement of the angular dependence of the Compton scattering cross section at various energies, fitting them with the predictions of χEFTs with polarisabilities as free parameters. The Compton scattering cross sections at HIγS are measured using liquid deuterium and 3He targets to substantially increase the beam-target luminosity. A set of large NaI detectors with unprecedented energy resolutions are also used. This setup is called the HIγS NaI Detector Array (HINDA) and has been successfully used to measure the Compton scattering cross sections on the deuteron and proton with plans to measure the cross sections using liquid 3He, a world first. This setup is shown in Fig. 2.
The HIγS and future medium-energy Compton gamma ray sources will enable high-precision measurements of the scalar and spin nucleon polarisabilities by Compton scattering from unpolarised and polarised targets. Such measurements, together with advances in calculations using lattice QCD and QCD-based effective field theories, will explore the QCD origin of nucleon structure as associated with the collective response of nucleons to electromagnetic impulses with unprecedented sensitivity.
Photodisintegration
The second low-energy QCD research programme using gamma rays at HIγS to probe the nucleon interactions is based on the process of photodisintegration. Before we discuss the details of photodisintegration of nuclei, we will first review the history of the strong interaction in relation to formation of light nuclei.
The famous alpha-particle scattering experiment by Ernest Rutherford in 1911 provided experimental evidence that led to his formulation of a model of the atom with most of the mass concentrated in a small volume at its centre, referred to as the nucleus. About a decade later, he performed measurements of alpha-particle induced reactions on light elements in which hydrogen nuclei (protons) were emitted, giving experimental evidence to the conjecture that the nucleus consists of protons. However, the mass of the protons only accounted for about half the mass of most elements. Rutherford hypothesised that the missing mass is due to an undiscovered particle that he named the ‘neutron’. His conjecture was that the neutron has about the same mass as the proton and is electrically neutral, which makes it difficult to detect. In addition, the neutrons would provide the extra attractive force needed to overcome the electric force repulsion of the protons inside nuclei.
In 1932, James Chadwick, a former student of Rutherford, discovered the neutron. This discovery, which earned him a Nobel Prize in Physics in 1935, completed the particle composition picture of the nucleus; it is composed of protons and neutrons, which are collectively referred to as nucleons. The fact that the Coulomb repulsion of the protons did not cause the nucleus to fly apart suggested that there was a new force acting inside the nucleus and that it was strong and short-ranged relative to the electric force. This new force was named the strong nuclear force at that time. The saturation of the binding energy per nucleon provided additional evidence that the strong nuclear force is short ranged.
The origins of nucleons and mesons
The first theory of the strong nuclear force was developed by Hideki Yukawa in 1935. His construction of the force was based on a field-theory approach in which the force between nucleons is due to the exchange of particles (bosons) in analogy to the electromagnetic force being caused by the exchange of photons. Yukawa postulated that the force carriers must have mass in order to create the finite range of the force and, using the Heisenberg uncertainty principle, he estimated the mass of the force carriers to be about 100 MeV/c2. These particles were called mesons. The lightest of these mesons, the pion, was discovered in cosmic-ray experiments in 1947. Yukawa was awarded the Nobel Prize in Physics in 1949 for this work.
Until the discovery of quarks in 1968, the meson exchange picture was the accepted theory of the strong nuclear force. It became clear that nucleons and mesons were composite objects composed of fundamental point-particles called quarks bonded by colour charge interactions mediated by the exchange of bosons called gluons. With these new insights, the force between nucleons was now recognised as not being a fundamental force, but rather a dynamical consequence of QCD.
Meson-exchange interactions, which for more than three decades were accepted as the solution to the nuclear-force problem, were relegated to being models – not theories – of the nuclear force. In QCD, the two-nucleon interaction is a six-quark problem that must be solved at low energies (long distances) where the colour interaction is strong and does not allow for use of perturbation methods. Nucleons are colour neutral, analogous to the interaction of electrically neutral atoms, the consequently static colour force between nucleons is zero. Therefore, the nuclear force between nucleons must be of a dynamic nature due to induced distortion of the colour charge inside the nucleons, behaving similarly to Van der Waals forces between electrically neutral atoms. There are two complementary approaches to solving low-energy QCD:
Lattice QCD consisting of brute-force computing done by putting the six-quark system on a four-dimensional lattice of discrete points that represents the three space and one time dimensions; and
Low-energy effective theories, in which effective degrees of freedom and interactions that are consistent with the properties of low-energy QCD are used.
Progress on both fronts requires a variety of high-quality data for properties of and reactions at low energies on light nuclei.
Innovation at TUNL
Researchers at TUNL use the unique monoenergetic photon beams at HIγS to measure reactions on light nuclei that probe nucleon interactions that are not accessible with two-nucleon scattering experiments, i.e., the neutron-neutron interaction and three-nucleon interactions. Three-nucleon interactions depend on the simultaneous co-ordinates and spin orientations of the three nucleons and cannot be represented by a series of two-nucleon interactions. Also, photonuclear reactions are sensitive to nuclear currents that are not accessible in pure hadronic processes.
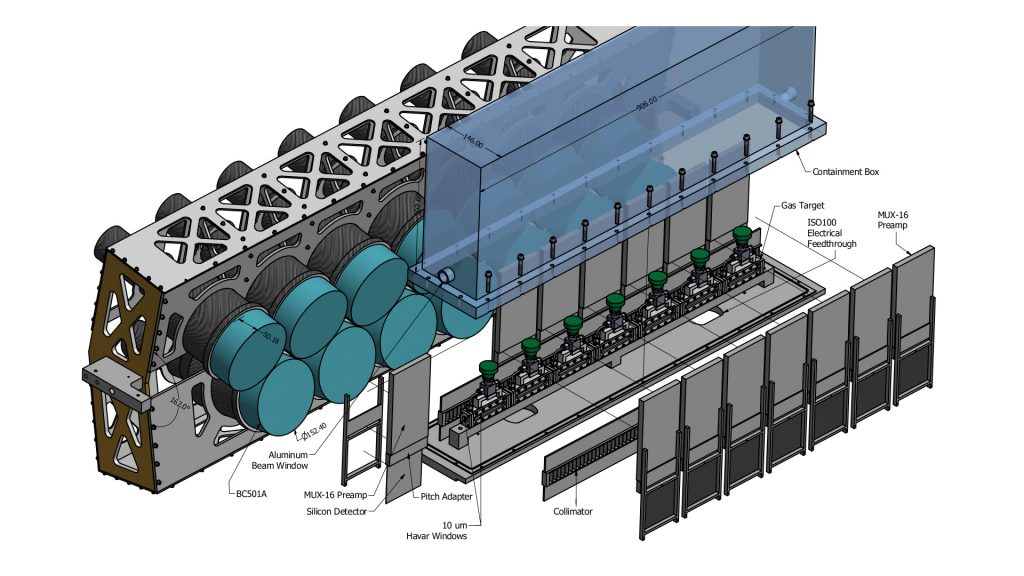
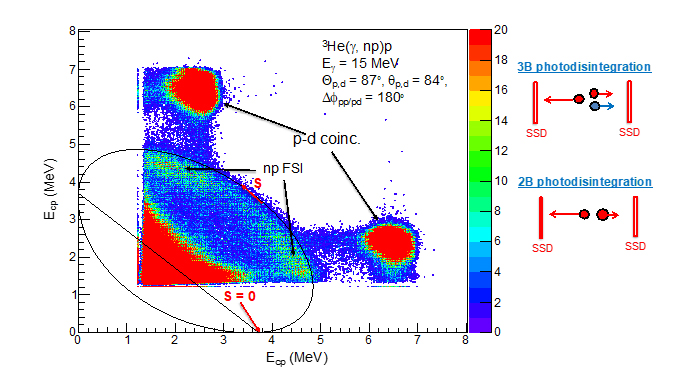
Photodisintegration measurements provide information about contributions from meson exchange currents (MEC) to the nuclear current operator. In three-nucleon (3N) systems, the effective current operator is the sum of the single-nucleon operators and the two- and three-nucleon operators, which are generally referred to as MECs where the two-nucleon operators are associated with pairwise nucleon-nucleon interactions and the three-nucleon current operators are due to three-nucleon interactions (3NIs). Accurate data for photodisintegration of 3N systems is important for evaluating and advancing ab-initio calculations. The first kinematically complete measurements of photodisintegration of 3He were recently measured at HIγS. A 3D rendering of the experimental setup is shown in Fig. 4, and an example of a two-dimensional histogram accumulated in the experiments containing events for three-body (proton-proton coincidences) and two-body (proton-deuteron coincidences) photodisintegration is shown Fig. 5. These measurements were performed with a 15.0-MeV γ-ray beam.
Please note, this article will also appear in the seventh edition of our quarterly publication.