Professor Dan Gabriel Cacuci highlights a breakthrough methodology which overcomes the curse of dimensionality while combining experimental and computational information to predict optimal values with reduced uncertainties for responses and parameters characterising forward/inverse problems.
The modelling of a physical system and/or the result of an indirect experimental measurement requires consideration of the following modelling components:
- A mathematical/computational model comprising equations (expressing conservation laws) that relate the system’s independent variables and parameters to the system’s state (i.e., dependent) variables;
- Probabilistic and/or deterministic constraints that delimit the ranges of the system’s parameters;
- One or several computational results, customarily referred to as ‘responses’ (or objective functions, or indices of performance), which are computed using the computational model; and
- Experimentally measured responses, with their respective nominal (mean) values and uncertainties (variances, covariances, skewness, kurtosis, etc.).
The results of either measurements or computations are never perfectly accurate. On the one hand, results of measurements inevitably reflect the influence of experimental errors, imperfect instruments, or imperfectly known calibration standards. Around any reported experimental value, therefore, there always exists a range of values that may also be plausibly representative of the true but unknown value of the measured quantity. On the other hand, computations are afflicted by errors stemming from numerical procedures, uncertain model parameters, boundary/initial conditions, and/or imperfectly known physical processes or problem geometry. Therefore, knowing just the nominal values of experimentally measured or computed quantities is insufficient for applications. The quantitative uncertainties accompanying measurements and computations are also needed, along with the respective nominal values. Extracting ‘best estimate’ values for model parameters and predicted results, together with ‘best estimate’ uncertainties for these parameters and results, requires the combination of experimental and computational data, including their accompanying uncertainties (standard deviations, correlations).
Predictive modelling
The goal of ‘predictive modelling’ is to obtain such ‘best estimate’ optimal values, with reduced uncertainties, to predict future outcomes based on all recognised errors and uncertainties. Predictive modelling requires reasoning using incomplete, error-afflicted and occasionally discrepant information, and comprises three key elements, namely: data assimilation and model calibration; quantification of the validation domain; and model extrapolation.
‘Data assimilation and model calibration’ addresses the integration of experimental data for the purpose of updating parameters underlying the computer/numerical simulation model. Important components underlying model calibration include quantification of uncertainties in the data and the model, quantification of the biases between model predictions and experimental data, and the computation of the sensitivities of the model responses to the model’s parameters. For large-scale models, the current model calibration methods are hampered by the significant computational effort required for computing exhaustively and exactly the requisite response sensitivities. Reducing this computational effort is paramount, and methods based on adjoint sensitivity models show great promise in this regard.
The ‘quantification of the validation domain’ underlying the model under investigation requires estimation of contours of constant uncertainty in the high-dimensional space that characterises the application of interest. In practice, this involves the identification of areas where the predictive estimation of uncertainty meets specified requirements for the performance, reliability, or safety of the system of interest.
‘Model extrapolation’ aims at quantifying the uncertainties in predictions under new environments or conditions, including both untested regions of the parameter space and higher levels of system complexity in the validation hierarchy. Extrapolation of models and the resulting increase of uncertainty are poorly understood, particularly the estimation of uncertainty that results from nonlinear coupling of two or more physical phenomena that were not coupled in the existing validation database.
The two oldest methodologies that aim at obtaining ‘best estimate’ optimal values by combining computational and experimental information are the ‘data adjustment’ method1,2 − which stems from the nuclear energy field − and the ‘data assimilation’ method2,3 − which is implemented in the geophysical sciences. Both of these methodologies attempt to minimise, in the least-square sense, a user-defined functional that represents the discrepancies between computed and measured model responses. In contrast to these methodologies, Cacuci4 has developed the BERRU-PM predictive modelling methodology by replacing the subjective ‘user-chosen functional to be minimised’ with the physics-based ‘maximum entropy’-principles, but is also inherently amenable to high-order formulations.
BERRU-PM Methodology
BERRU stands for ‘Best-Estimate Results with Reduced Uncertainties’, because the application of the BERRU predictive modelling (PM) methodology reduces the predicted standard deviations of both the best-estimate predicted responses and best-estimate predicted parameters. The BERRU predictive modelling methodology also provides a quantitative indicator, constructed from response sensitivities and response and parameter covariance matrices, for determining the consistency (agreement or disagreement) among the a priori computational and experimental information available for parameters and responses. This consistency indicator measures, in a chi-square-like metric, the deviations between the experimental and nominally computed responses and can be evaluated directly from the originally given data (i.e., given parameters and responses, together with their original uncertainties), once the response sensitivities have become available. Furthermore, the maximum entropy principle underlying the BERRU-PM methodology ensures that, the more information is assimilated, the more the predicted standard deviations of the predicted responses and parameters are reduced, since the introduction of additional knowledge reduces the state of ignorance (as long as the additional information is consistent with the physical underlying system), as would also be expected based on principles of information theory. The BERRU-PM methodology generalises and significantly extends the customary data adjustment and/or 4D-VAR data assimilation procedures.
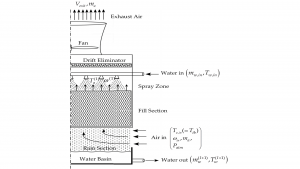
Typical results predicted by the BERRU-PM methodology are depicted in Fig. 1 and Fig. 2, which illustrate the improvement provided by the BERRU-PM methodology4 using the digital twin model of a mechanical draft (counter-flow) cooling tower at the Savannah River National Laboratory (USA). This digital twin comprises over 100 uncertain parameters which affect appreciably the computed model responses (outlet air humidity, outlet air, and outlet water temperatures). The BERRU-PM methodology combines optimally computational information with actual field measurements of responses (comprising 8,079 measured datasets of outlet air humidity, outlet air, and outlet water temperatures). In the ‘forward-mode’, the BERRU-PM methodology reduces the predicted uncertainties for these responses at the locations where measurements of the quantities of interest are available to values that are smaller than either the computed or the measured uncertainties. Simultaneously with the ‘forward-mode’, the ‘inverse-mode’ BERRU-PM methodology reduces the uncertainties for quantities of interest inside the tower’s fill section, where no direct measurements are available. This is a general characteristic of the BERRU-PM methodology, which simultaneously reduces uncertainties, not only at the locations where direct measurements are available, but also at locations where no direct measurements are available.
The reliability of the model
Analysing the reliability of the model results requires the computation and use of the functional derivatives (called ‘sensitivities’) of the model’s response to the model’s imprecisely known parameters. Model parameters also include imprecisely known internal and external boundaries that characterise the physical system represented by the respective model. The sensitivities of responses to model parameters are needed for many purposes, including:
- Understanding the model by ranking the importance of the various parameters;
- Performing ‘reduced-order modelling’ by eliminating unimportant parameters and/or processes;
- Quantifying the uncertainties induced in a model response due to model parameter uncertainties;
- Performing ‘model validation’ by comparing computations to experiments to address the question ‘does the model represent reality?’;
- Prioritising improvements in the model;
- Performing data assimilation and model calibration as part of ‘forward and inverse modelling’ to obtain best-estimate predicted results with reduced predicted uncertainties; and
- Designing and optimising the system.
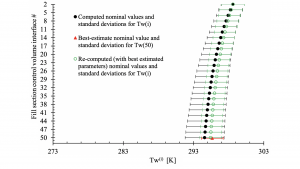
values) nominal values and standard deviations for the water temperature, Tw(i) (i=2,…,50), at the exit of
each of the 50 control volumes along the height of the fill section of the cooling tower
The computation of sensitivities by conventional deterministic and/or statistical methods, which require repeated re-computations using the original model with altered parameter values, is easy to implement but can provide only approximate, rather than exact, values for the sensitivities. Furthermore, since the number of sensitivities increases exponentially with the order of the respective sensitivities, conventional methods can only be used for models with few parameters and only for very low order (typically first-order) sensitivities, since the number of computations needed for obtaining higher-order sensitivities by conventional methods becomes impractical for realistic models because of the well-known ‘curse of dimensionality’.5
Nth-CASAM and Nth-BERRU-PM
The only computational methodology that yields exact values for the sensitivities of all orders while overcoming the curse of dimensionality is the ‘Nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology (nth-CASAM)’ developed by Cacuci6-8 by generalising his original pioneering work.9 The number of computations required by the nth-CASAM increases linearly in alternative Hilbert spaces rather than exponentially in the original Hilbert space. The development of the nth-CASAM has made it possible to perform high-order sensitivity analysis and uncertainty quantification for large-scale systems, as illustrated on the OECD/NEA reactor physics benchmark model,8 which involves 21,976 uncertain model parameters. The development of the nth-CASAM has, in turn, opened the possibility of significantly extending the scopes of other methodologies which need high-order sensitivities. In particular, the availability of arbitrarily high-order exact sensitivities computed using the nth-CASAM has opened the possibility of extending the BERRU-PM methodology to higher-order. This activity is currently underway and is expected to produce an arbitrarily high-order predictive modelling methodology (nth-BERRU-PM), which is expected to overcome the curse of dimensionality in predictive modelling.
The revolutionary consequences of the availability of the nth-CASAM and nth-BERRU-PM methodologies will be demonstrated by combining these methodologies with neural nets (Artificial Intelligence) aiming at creating digital twins for simulating any process on Earth with the highest conceivable accuracy and quantified uncertainties of any order. The resulting high-order Artificial Intelligence (AI) digital twins are envisaged to harness the massive power of the new AI computers (e.g., the Cerebras~1 Million AI cores on a single computer chip). Future generations of parallel computers may comprise millions of such Cerebras chips, and the computations may be even more distributed than presently. For example, certain computers would perform computations using the world’s financial/economic models, while other computers would perform computations using physical models, with linkages between these models, (all models being components of a high-order AI planet Earth simulator). One would be able to examine ‘what if’ scenarios, such as: What would happen if we took away some of the CO2 from the atmosphere in terms of our weather and climate change? What would happen if a new virus emerged? What would happen if we developed a new product or changed the financial system in a business, country, or the world? However, one could go beyond ‘what if’ scenarios and optimise the businesses, their products, the climate, and the way we live − as well as the data we collect to help perform this optimisation. For example, in designing new cities, buildings and power plants, high-order AI digital twins will enable the subsequent optimisation of the respective plant or building, making them much more efficient and safer. Such high-order AI digital twins will be linked together to construct, brick-by-brick, a high-order AI planet Earth simulator, while enabling researchers/industrialists to use the various components, along the way, to optimise specialised problems of interest.
References
- Gandini, A.; Petilli, M. AMARA: A code using the lagrange multipliers method for nuclear data adjustment. CNEN-RI/FI(73)39, Comitato Nazionale Energia Nucleare, 1973, Casaccia/Rome, Italy
- Cacuci, D.G.; Navon, M.I.; Ionescu-Bujor, M. Computational Methods for Data Evaluation and Assimilation. Chapman & Hall/CRC, Boca Raton, USA, 2014
- Lewis, J. M., Lakshmivarahan, S., and Dhall, S.K., 2006. Dynamic Data Assimilation: A Least Square Approach. Cambridge University Press, Cambridge, UK, 2006
- Cacuci, D.G. BERRU Predictive Modeling: Best-Estimate Results with Reduced Uncertainties. Springer, Berlin, Germany, 2019
- Bellman, R.E. Dynamic programming. Rand Corporation, Princeton University Press, ISBN 978-0-691-07951-6, USA. 1957
- Cacuci, D.G. Second-order adjoint sensitivity analysis methodology (2nd-ASAM) for large-scale nonlinear systems: I. Theory. Nucl. Sci. Eng. 2016, 184, 16–30
- Cacuci, D.G. The nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology: Overcoming the Curse of Dimensionality. Volume I: Linear Systems; Volume III: Nonlinear Systems. Springer Nature Switzerland, Cham, Switzerland, 2022
- Cacuci, D.G. and Fang, R. The nth-Order Comprehensive Adjoint Sensitivity Analysis Methodology: Overcoming the Curse of Dimensionality. Volume II: Application to a Large-Scale System. Springer Nature Switzerland, Cham, Switzerland, in print, 2023
- Cacuci, D.G. Sensitivity theory for nonlinear systems: I. Nonlinear functional analysis approach. J. Math. Phys., 1981, 22, pp. 2794–2812. See also: Práger, T. and Kelemen, F. D. Adjoint methods and their application in earth sciences. Chapter 4, Part A, pp 203-275, in Faragó, I.; Havasi, Á.; Zlatev, Z. (Eds.) Advanced Numerical Methods for Complex Environmental Models: Needs and Availability, Bentham Science Publishers, Bussum, The Netherlands, 2013
Please note, this article will also appear in the thirteenth edition of our quarterly publication.





