Dr Adam Smith, Royal Commission for the Exhibition of 1851 Research Fellow 2020, discusses developments in the evolution of computing and how quantum computers have the potential to revolutionise it further.
Quantum computing has always been accompanied by a lot of hype, and this has been growing faster than ever over the past few years. It has enticed investment from universities, multinational companies, and governments across the world.
There is palpable excitement over the evolution of computing, with promises ranging from new cancer-defeating drugs to powerful quantum Artificial Intelligence. It is very easy to get swept up in all this excitement, but let us take a moment to ask some questions: What is a quantum computer? Why do we need one? And why don’t we have one yet?
Although we may not realise it, quantum physics has already revolutionised our daily lives. Nowhere is this more direct than in the billions of transistors that we carry in our pockets inside our smartphones.
That these work – and allow us to spend hours a day on social media – is ultimately due to the quantum mechanical behaviour of nature. Up to now, quantum mechanics has allowed us to understand natural phenomena and to take advantage of them. As we enter the ‘second quantum revolution’, our goal is to control quantum mechanics and get it to do even more useful things for us.
One of the most general ways to do this is to build a quantum computer that harnesses the properties of quantum mechanics.
Why do we need quantum computers?
The most important thing to appreciate about quantum computers is that they are not just faster computers.
In fact, for many tasks, the computers we already have will be far faster, with the evolution of computing having already gone through more than half a century of development and refinement.
Most simply put, quantum computers work in a completely different way from existing computers. However, because of this radically different approach to computing, there are some tasks quantum computers will allow us to solve that have so far been impossible.
What exactly are these computers good at? More critically, why do we need one? The example that is often given is their ability to crack the communication encryption methods we currently use, and the resulting need for new quantum encryption.
While this is a very interesting problem in quantum information and mathematics, I find this about as comforting as saying that a nuclear deterrent is the best defence against nuclear weapons. These applications are many years away and depend on large-scale error-resistant quantum computers.
What I find infinitely more exciting, is the prospect that quantum computers could improve our everyday lives. The evolution of computing can help us design new materials with remarkable properties, such as superconductivity – characterised by zero electrical resistivity.
Such materials would allow our transport, computers, and power supplies to be faster, more energy efficient, and cheaper to run. Even more impactful would be the design of new drugs to save lives. New drugs could be more effective, potentially eradicate cancers, and result in cheaper mass production to save lives in impoverished countries.
This is not just unfounded wishful thinking: it is believed that these will be some of the first practical applications of quantum computers. Before jumping into how all of this could be possible, let us start with some basics.
What are quantum computers?
Rather than talking in terms of abstract quantum mechanical concepts, it is more instructive to explain how real quantum computers actually work – with some musical analogies along the way.
For concreteness, I will focus on a particular technology – adopted by Google, IBM, and many others – based on superconducting circuits.
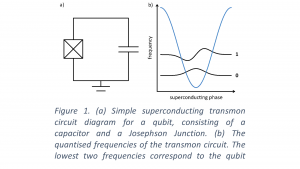
The building block of a quantum computer is a qubit. A qubit is a small electrical circuit in which current oscillates at very specific frequencies. We can think of this qubit circuit in a very similar way to the strings on a guitar. Because the strings of a guitar are fixed at the ends, they can only vibrate at specific frequencies. A physicist would say that the frequencies of the string are quantised, and a musician would call these quantised frequencies ‘harmonics’. Essentially, only certain frequencies can fit onto the string with fixed ends.
Similarly, the qubit is quantised: it can only oscillate at certain frequencies. Just like the guitar strings, the qubit circuit can oscillate with many different frequencies. To make programming and engineering a quantum computer simpler, we focus only on the lowest two frequencies, which are labelled 0 and 1 in analogy with traditional computing.
When we play the guitar string, it vibrates with lots of these harmonic, quantised frequencies at once. Playing the same note on a violin will give a slightly different combination of frequencies, which is why they sound different to us. A qubit can also vibrate with a mixture of frequencies at the same time. This is the first main ingredient of quantum mechanics: quantum superposition. While this is often a large conceptual hurdle for understanding quantum mechanics, I would argue that this is not so unfamiliar when we have the analogy of guitar strings in mind.
The weirdness of quantum mechanics comes when we consider quantum measurements. When we measure a qubit, it will collapse into only one of its possible frequencies. Unlike the guitar string, we can’t measure (hear) all the frequencies (harmonics) at the same time. Furthermore, it will do this probabilistically.
You would be excused for not believing this surprising randomness of nature since even Albert Einstein struggled with it, famously quoted as saying that “God does not play dice with the Universe”. It turns out that quantum mechanics is the most accurately verified theory of nature that we have, and it is fundamentally probabilistic.
The reason this does not correspond to our everyday experience of the world is simply a question of scale: while the position of an individual atom is determined probabilistically when we look at it, the average position of all the gargantuan number of atoms that make up everyday objects is effectively deterministic.
This is much like how a casino works: while an individual win or loss is probabilistic, once you’ve averaged out and looked at the scale of the whole casino, you’ll find the casino always wins.
A quantum computer with a single qubit is not very useful, and we can simulate this efficiently on a laptop. The power of a quantum computer comes when we introduce many coupled qubits. When we couple qubits, we can end up with situations that are impossible to describe without quantum mechanics.
If we have two qubits, then we can create a setup where they are quantum entangled. When qubits are entangled, we can no longer talk about the qubits separately. Instead, we must talk about the state of the two qubits as one collective system. Entangled qubits will remain entangled no matter how far you separate them. Moreover, if we do something to one qubit, such as measuring it, then this will instantaneously affect the other qubit.
This ‘spooky action at a distance’ was another aspect of quantum physics that troubled Albert Einstein – so you are in good company if you find it unbelievable. Nevertheless, this is how the world works, and quantum entanglement is the main resource of quantum computers that allows them to perform tasks impossible for standard computers.
Quantum entanglement makes things a lot more complicated. If I wanted to tell you what the current state of my quantum computer is, then I would need to know the probability of measuring every one of the possible qubit combinations. The amount of information I would need to give you grows exponentially with the number of qubits. This is in stark contrast to a standard computer, where I would simply give you a list of 1s and 0s corresponding to the classical bits.
You will have, no doubt, encountered exponentials at some point. However, I believe nobody ever really grasps how fast exponentials grow, but there is a classic story that does a good job of capturing it.
The story is about a King who challenges one of his subjects to a game of chess and offers a prize of their choice if they win. The subject, to the surprise and delight of the King, asks for rice but counted in a very specific way. One grain for the first square on the board, two on the second, four on the third, eight on the fourth, and so on, doubling for each square. After losing the game, the King begins counting out the rice but gets worried when he reaches one million by only the third row. After consulting his mathematicians, the king is informed that he would need approximately 210 billion tonnes of rice! Even with today’s levels of rice production, this would take almost two millennia to grow.
The main takeaway from this is that rather than quantum computers being super-fast computers, they work very differently from classical computers. A classical computer works with many independent bits that can each be in two possible states: 0 and 1. In a quantum computer, it is instead all the exponentially many combinations of the qubit states that are important.
For many tasks, this explosion in complexity is unnecessary, and can even be detrimental. We also don’t have direct access to all these combinations, since whenever we measure, the state collapses. However, for certain tasks, and through very clever manipulations, a quantum computer can solve tasks exponentially faster than its classical counterpart. This is why there is so much hype and investment in the evolution of computing.
What is a quantum computer good for?
At the heart of the revolutions in materials science and drug discovery that quantum computing promises, is quantum many-body physics. The collective behaviour of many-body systems can be far richer than the individual constituents.
Dramatic and familiar examples include the communities, governments, and cities that humankind has created, which are the result of interactions between huge numbers of people over large periods of time. Similarly, the properties of materials, and the interactions that drugs have in our body, are ultimately the result of quantum mechanical interactions between incredible numbers of microscopic particles. This richness of this collective behaviour is mirrored by the difficulty we have in understanding and controlling it. What is so exciting is that these are exactly the kinds of problems quantum computers are good at.
The basic approach to these complex problems has three main steps. First, we start with a model. For example, this could be a simplified description of the atoms in a material that we want to understand. Due to the collective behaviour of these models, a simple model can lead to very complicated behaviour.
That’s where step two comes in: we find a way to map this model onto the quantum computer. This is essentially designing a quantum algorithm to simulate the properties of our model.
Finally, in step three, we use the predictions that our quantum computer allows us to make and compare with real experiments on the material we want to understand. If the predictions don’t match, we go back to the first step, tweak our model, and repeat the process.
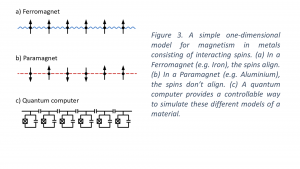
Let us consider a more concrete and very simplified example (that doesn’t actually require a quantum computer) to understand why some metals are magnetic. The first step is the model. Let’s imagine that every electron in the metal has a tiny bar magnet attached to it that can point up or down. These little magnets also prefer to be pointing in the same direction as their neighbour.
While this might sound like a silly model, it turns out to capture the magnetic behaviour of many common metals. This model is also very simple to map to a quantum computer. Each little magnet that can point up or down gets mapped to a qubit that can be in the state of 1 or 0.
By controlling the coupling between our qubits we can entangle them, making them have a higher probability of being measured in the same state. Finally, the simulation on the quantum computer will predict that if we bring a magnet next to the metal, all the little bar magnets will point towards it and get attracted. We would have then successfully predicted Ferromagnetism, which is why steel (iron-based) objects such as paperclips or your fridge are attracted to magnets. If we wanted to understand why an Aluminium fizzy pop can is not attracted to a magnet, we would have to modify our model and repeat the process.
This approach of coming up with models and matching predictions with real materials has been extremely successful in the evolution of computing. The problem is that we have mostly run out of simple models that we can easily solve to make these predictions. The reality is that when new materials or drugs are discovered, it is only much later that we understand how they work.
Rather than spending lots of money and trial and error to create new materials, current research aims to use quantum computers to simulate their properties. This could allow us to only synthesise those that behave the way we want. This could be even more powerful in the context of drug discovery, where potential side effects can take years to emerge. This type of simulation could discount dangerous drugs at an early stage and guide us to synthesise useful ones.
Delays in the evolution of computing
What is most exciting about quantum computers is they do already exist! There are now many quantum computers based on various technologies around the world.
The evolution in computing has been nothing short of incredible. Existing quantum computers are the most well-isolated and precisely controlled quantum systems that have ever been made. Despite this impressive technical achievement, the reality is that more than half a century of development has resulted in traditional computers that are still the most practical approach for the problems quantum computers promise to solve. Limiting progress are two major hurdles that we need to overcome: noise and scale.
In a quantum computer, we must face noise in many ways. Firstly, for a device to even behave in a quantum mechanical way, we must cool it down, below -273°C, so that it is one of the coldest places in the Universe. We also need to completely shield it from everything that could interfere with it – from mobile phones to cosmic rays. Even if we could create a perfect shield, there can be noise in the wires we use to control the device, the chip itself will naturally have imperfections, and there will be unintentional coupling between qubits.
The engineering task demands a level of control of quantum systems far beyond anything mankind has achieved before in the evolution of computing.
There is a solution to the noise problem, at least theoretically, which is error correction. The basic idea is to replace one qubit with many qubits, all of which should collectively be in the same state if the computation is implemented correctly.
This allows us to detect when the qubits disagree with each other, indicating that an error happened somewhere in the computation. By doing this in a clever way, we can even figure out exactly what error happened and when allowing us to correct the computation. Quantum error correction is one of the main goals in the evolution of computing, but it requires many more qubits.
The good news is that we don’t need to wait. Since we are evolving models of complex systems that must function in the noisy, imperfect real world, we can handle a bit of noise in our quantum computers. While quantum error correction is crucial for many applications of quantum computers, pioneering research aims to extract the most out of the small and noisy quantum computers that will be available in the very near future.
We need to remind ourselves that quantum computing is still in its infancy. Having gone through this long process for traditional computers – from room-sized valve-based calculators to pocket-sized smartphones with billions of transistors – allows us to have the foresight of how much progress there is to come in the evolution of computing, and how much it can improve our lives.