The University of Maryland highlights light’s importance in physics, focusing on electromagnetic waves, special relativity, quantum mechanics, and upcoming virtual matter experiments to explore the quantum vacuum’s mysteries.
This is a story about light, matter and light-matter interaction to awaken the quantum vaccuum. Most of you reading this article have had encounters with light. Light has been indispensable to life in countless ways, whether it has been feeling the sun’s warmth, peering at stars in the night sky, or sitting around a campfire.
But this story is not about the virtues of light in everyday life; rather, it is about how light has been instrumental in guiding and improving our scientific understanding of the Universe. We will narrow the scope from science in general to physics in particular. We will further hone in on four subjects and their interconnectedness – electromagnetic waves, special relativity, quantum mechanics and virtual matter.
An electromagnetic wave is a fancy way physicists refer to light, because it is a cooperative union of oscillating electric and magnetic fields. Its spectrum ranges from the ultralow-energy radio waves to the extremely high-energy gamma rays. The visible spectrum occupies a tiny sliver in between. Special relativity describes the relationship between space and time and introduces the universal speed limit, the speed with which light travels in a vacuum. Even matter obeys this speed limit.
Quantum mechanics best describes the microscopic world of atoms and molecules. Generally, we do not experience quantum mechanics directly in the macroscopic world of everyday life; however, examples exist. The virtual matter will be the principal character in two forthcoming experiments the physics community is actively preparing to perform in the not-too-distant future and the subject of the last two chapters. If you permit me to do so, I will delay defining virtual matter until later in our discussion.
This narrative aims to give you, the reader, a glimpse at how physicists plan to employ light – laser light, extreme laser light – to agitate the quantum vacuum. This will be possible by performing experiments under conditions in the laboratory, which usually can only be found in astrophysical systems.
These environments are responsible for some of the spectacular images the Hubble and James Webb space telescopes obtained. Laboratory-based experiments will enable physicists to address questions nearly a century old and might even shed light on more contemporary puzzles like dark matter.
Along the way, we will review some history that has contributed to the knowledge that enables this pursuit. Throughout our discussion, we will rely on one of the favourite tools of physicists – models – to aid understanding. So, grab your favourite drink and snack, and join us on this journey.
How light was instrumental in changing the view of matter and radiation
One hundred years ago, the imminent physicist and Nobel Laureate (for his work leading to his discovery of the electron in the late 1800s), Sir JJ Thomson, was credited with stating: ”The study of light has resulted in achievements of insight, imagination and ingenuity unsurpassed in any field of mental activity; it illustrates, too, better than any other branch of physics, the vicissitudes of theories.” His statement is no less true today than it was then. Of course, light goes back to the beginning as we know it. We read in Genesis 1:1, for example: “In the beginning … darkness was over the face of the deep. … And God said, ‘Let there be light,’ and there was light.”
Since the Big Bang, light has been a fundamental tool to effectuate knowledge and create technology. Early on, humans marvelled over lights in the sky, curious about what they were and, in some cases, what they meant. Patterns could be recognised, and ancient communities even built monuments to celebrate daily and annual repeating events.
One could argue that contemporary communities do the same; they call them observatories. The best they could do in centuries past was to work out the celestial mechanics, which is actually quite impressive. But, observing the diversity of spectacular astrophysical events and understanding the physics under the hood driving them had to wait for more powerful instrumentation and scientific revelation.
Back a century again, the needed revelation was afoot – the development of quantum mechanics – which completely changed how physicists viewed the world. This was induced in large measure by the confusing nature of light, sometimes behaving as a wave and sometimes as a particle – corpuscle.¹
In 1704, Issac Newton pushed the idea of the corpuscular nature of light in Opticks. The corpuscle idea was all but abandoned after Thomas Young² demonstrated wave interference about a century later. In the late 1800s, physicists believed that the world was divided neatly into two categories: things were either matter or waves, but not both.
Things began to get complicated moving toward and into the twentieth century with reports of results that had light fitting into the corpuscular categories. A corpuscular nature of light was needed, for example, to explain the photoelectric effect³ and black-body radiation.⁴
Things spiralled further downhill because it was not just light that was exhibiting this disturbing, schizophrenic behaviour; matter was misbehaving as well. Radiation (light) was observed from atoms that were believed to be due to electrons circling the nucleus like planets circle the Sun; this would later become the basis of the Bohr model of the atom. It was well known then that electrons experiencing a force will radiate – give off light. A radiating electron gives up some of its energy. Electrons moving in circles will radiate.⁵
Consequently, at the time, physicists expected any radiation coming from an electron orbiting in an atom to be continuous. However, discrete wavelengths were observed. Even more perplexing, the wavelengths fit empirical formulae that suggested that the electrons could only have certain energies. This bewilderment was mentioned in a Louis de Broglie Nobel Lecture: He said: “The necessity of assuming for light two contradictory theories – that of waves and that of corpuscles – and the inability to understand why, among the infinity of motions which an electron ought to be able to have in the atom according to classical concepts, only certain ones were possible: such were the enigmas confronting physicists at the time I resumed my studies of theoretical physics.”
The state of physics at that time was quite unsettling. Light was straddling two presumed mutually exclusive categories. Electrons attached to atoms were exhibiting quantised energies. In addition, de Broglie suggested that matter, too, could have a wavelength.
A more profound understanding of the physics was possible by a deeper appreciation of the mathematics undergirding the existing theories.
In his Nobel Lecture, Erwin Schrödinger (one of the founding fathers of quantum mechanics) credits light for the inspiration of his work. Schrödinger is responsible for one of the famous equations in quantum mechanics – the Schrödinger Equation. He describes his fascination with the mathematical similarity between Fermat’s Principle (due to Pierre de Fermat in the mid 1600s) about the time it takes a ray of light to travel from one point to another and Hamilton’s Principle (due to William Rowan Hamilton in the early part of the 1800s) about the relationship between kinetic energy and potential energy. (Kinetic energy is due to motion while potential energy is related to the forces acting on matter that can cause motion but has not yet.)
Fermat’s Principle governs the trajectory light rays take, which explains, for example, refraction (the bending of light going from air into glass) that causes a prism to disperse light into a rainbow of colours. Hamilton’s Principle governs the trajectory matter takes when experiencing forces and describes, for example, the orbits of planets.⁶
What Schrödinger found intriguing was that while Fermat’s Principle did not apply to waves, it predicted some important aspects of the behaviour of light waves – refraction, as we stated above. In the latter part of the 1600s, waves were known to be governed by Huygens’ Principle (due to Christian Huygens). It was quite insightful of Schrödinger to consider light rays as a model for light waves; after all, he did not have the benefit of laser beams as we do today.
This insight prompted him to say: “It seemed as if Nature had realised one and the same law twice by entirely different means: first in the case of light, by means of a fairly obvious play of rays; and again in the case of the mass points, which was anything but obvious, unless somehow wave nature were to be attributed to them also.”⁷
The conjecture is that because nature gave clues about light as a wave through a model of light as a ray, perhaps that connection was also active for the nature of matter – matter as a particle giving clues to matter as a wave. Again, it is the striking mathematical similarities between Fermat’s and Hamilton’s Principles that led to Schrödinger’s statement and eventually to matter waves.
The Schrödinger Equation describes the dynamics of matter waves in quantum mechanics in a similar way that Newton’s Equations describe the motion of matter as particles. The wave nature is essential for a correct description of electrons in atoms. The Bohr model of the atom treats electrons as localised particles orbiting at a specific radius from the nuclear, again like planets orbiting the Sun.
In distinction, solving the Schrödinger Equation for an electron in the atom leads to a probability distribution of finding the electron. Physicists often picture (model) this probability distribution as a delocalised cloud with the electron everywhere within the cloud at the same time.
It turns out that the Bohr model of the hydrogen atom correctly predicts many of the energy states of the electron (recall they are quantised), its speed and the average radius of the electron’s orbit.
We have already discussed three models that have been extremely valuable in physics for extracting the essence of a phenomenon even when the model is not precisely accurate. It is important to understand, however, that models are useful but tend to break down – fail to give reasonable answers – when pushed beyond their limits of applicability.
It is often very beneficial to look at a problem from different angles. Nobel Laureate Werner Heisenberg developed a different view of quantum mechanics.⁸ His approach gives the same answers as Schrödinger’s approach but leads to the famous Uncertainty Principle.
The Uncertainty Principle sets a fundamental limit on the accuracy with which two observables, like position and momentum, can be known simultaneously. Unlike classical mechanics, where position and momentum can be determined with arbitrary accuracy simultaneously, quantum mechanics dictates that the more accurate one’s knowledge is of one observable (say position), the less accurate the other (say momentum) can be.
The Uncertainty Principle explains why the position of the electron is not determined precisely in the hydrogen atom. Because the energy, which is proportional to the square of the momentum, is determined well, the electron’s position cannot be determined well at the same time. Hence, the cloud. This first quantum revolution completely changed how physicists viewed the world.
The laser as a precision tool to explore novel quantum physics
Quantum mechanics has led to a very detailed description of the building blocks of the material world – atoms and molecules – and explanations for a variety of phenomena, for example, superconductivity (a macroscopic example of quantum mechanics). Quantum mechanics is responsible for the development of a number of quantum-based technologies. Today, we find ourselves in a second quantum revolution, with quantum being shown virtually everywhere.
In addition to quantum technologies being tools themselves, they have also fueled new research directions, like cooling atoms with lasers, and have enabled additional spin-off technologies. It is fair to say the most well-known quantum device, if not ubiquitous in society, is the laser, which is the protagonist of the rest of our story. By the way, the laser is another macroscopic example of quantum mechanics.
Lasers have come a long way since their inception some 65 years ago. They are the primary tool in investigations ranging from ultrasensitive metrology to ultrafast dynamics and control to preparation of extreme conditions for novel studies.
The last one is the primary driver for what we will now present. Contemporary laser technology allows pulses to be generated on the multi-petawatt level, where 1 petawatt (PW) is equal to 1 billion times 1 million Watts⁹ of power in the form of light. These pulses are packaged to last only a few tens of femtoseconds.

To put this time scale into perspective, 1 fs is to 1 s as 7 ¼ min is to the age of the universe, about 13.8 billion years. The total energy in a 10 PW, 25 fs pulse is about 200 times less than the energy stored in an average cell phone battery today. This seems pretty minuscule.
What is the big deal, you ask? Well, total energy is not the whole story of what we want to discuss below. It is really about how much energy can be delivered to a small spot in a short amount of time. That is the energy per unit time, per unit area – intensity. The quality of pulses that can be generated today is so high that they can be focused to very, very tiny spots. The focal spots can be just a few microns in diameter (about the size of a bacterium).
Concentrating the light of what appears to be a negligible amount of energy can produce intensities so high that it will destroy any material placed in its path. In addition, intensities sufficient to perturb the vacuum are anticipated to be available in the near future. The quantum vacuum is where virtual particles live, which we have yet to define.
From non-relativistic to relativistic quantum mechanics
To understand how the vacuum is perturbed by focused laser-light pulses, a bit more background is needed. We begin by considering Fig. 1, which shows how electrons respond in light fields at various intensities. We choose electrons because light interacts primarily with electrons when absorbed by atoms, molecules and solids.
Let me stop for a moment and tell you a little more about light. At the beginning, I mentioned that light is made up of oscillating electric and magnetic fields. Of these, the magnitude of the electric field is stronger than that of the magnetic field by a factor of about 300 million! The interaction between the electron and the electric field is proportional to the strength of the electric field. The interaction between the electron and the magnetic field is proportional to the electron’s speed times the magnetic field strength.
The Schrödinger Equation is generally applied to light absorption in matter in the two lowest regimes in Fig. 1, where electrons move at non-relativistic speeds – i.e., the speeds are much, much less than the speed of light. An important consequence of low speeds is that the force on electrons is due almost exclusively to how the electrons interact with the electric field of the laser. The force due to the magnetic field is almost negligible.10 These two lower regimes are generally the regimes of atomic, molecular and optical physics research where the Schrödinger Equation gives reasonable results.
A transition to the relativistic regime occurs when the electron’s speed is very close to the speed of light, closing the gap of 300 million between the magnitudes of the electric and magnetic forces. Hence, the magnetic force on the electron is no longer negligible. Dynamics induced by the laser must explicitly include both the electric and magnetic forces. There is no specific value that demarks the relativistic speed threshold. One definition often used is when the electron’s speed is about 43% of the speed of light, which corresponds to when the kinetic energy of the electron is equal to its rest-mass energy;11 this threshold is shown in Fig. 1. The magnetic force is odd in that the direction of the force is perpendicular to both the direction of the magnetic field and that of the electron’s motion. The magnetic force can significantly change aspects of light-matter interaction with atoms and molecules.
In the relativistic regime, the equations of motion valid for non-relativistic speeds must be modified for a correct description. The necessary modifications are contained in Einstein’s Theory of Special Relativity. Shortly after the development of the nonrelativistic matter wave equation (Schrödinger Equation), an effort was made to develop a relativistic version of the wave equation. The relativistic version consistent with special relativity that applies to electrons is the Dirac Equation. In addition to being fully relativistic, the Dirac Equation accounts for a fundamental property of electrons that the Schrödinger Equation does not, something called spin. Spin is an internal quantum property of the electron of which there is no classical analogue. While spin can be inserted artificially into the Schrödinger Equation, it is inherent in the Dirac solution.
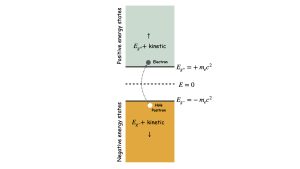
The Dirac Equation has four solutions – two correspond to the electron’s energy and two to its spin states. The energy in special relativity includes both rest-mass energy and kinetic energy; even a particle that is stationary will have its rest-mass energy.
The odd thing about Dirac’s two energies is that one is negative,12 even for an electron at rest (see Fig. 2). These negative energies were concerning for at least two reasons. First, their interpretation was not clear at first. How, for example, can the rest-mass energy be negative; what does that even mean, physically?
Second, if we accept these negative-energy states, that leads to another problem because they have less energy than all the positive-energy states. In principle, the number of possible negative-energy states is unlimited, as are the number of positive-energies states. Because systems tend to relax to lower energy states when available, it was puzzling why electrons did not relax into the negative energy states.
To solve the second dilemma, Dirac had a brilliant idea; he postulated that all the negative-energy states must be filled with electrons. He called this the negative-energy sea – it is sometimes referred to as simply the Dirac Sea. If all the negative-energy states were filled with electrons, the Pauli Exclusion Principle12 would prevent any other electrons from relax to those states.
While the Dirac Sea explains why electrons do not relax to negative-energy states, it does not address how electrons in the Sea should be interpreted. To handle that, Dirac further postulated that because the energies are negative, these electrons must not be observable directly – they must be virtual.
So, for our purpose, virtual electrons have negative energy and are not observable directly; however, as we will discuss below, they can influence what is observed experimentally.
Virtual particles and quantum fluctuation
Fig. 2 shows that there is a large energy gap between the positive-energy states and negative-energy states, with a gap spacing equal to twice the rest-mass energy of the electron. It did not take physicists long to speculate about exciting an electron from the negative states to the positive states with light, just like exciting electrons from a lower state to an upper state in an atom with light.
In the process, as indicated in Fig. 2, a hole in the negative energy states would be left behind. Dirac interpreted the hole left behind as a new particle, an antiparticle to the electron and called a positron. Both the electron and the positron would be detectable as real particles.
A possible experiment was first proposed in the early 1930s by J. Robert Oppenheimer and Milton S. Plesset. Such an experiment would create an electron-positron pair. Antimatter, by the way, has the opposite properties to that of matter. For example, the positron has a positive charge because the electron has a negative charge. Consequently, when a particle and its antiparticle encounter each other, they annihilate each other – disappear from existence – and give up their rest-mass energy back as light. Annihilation is the opposite process of matter-antimatter creation. Thus, the Dirac Equation gave birth to virtual particles, antimatter and dreams of creating matter from the Dirac Sea. The modern dream of particle-pair creation will be discussed in the last section. But first, we need to introduce another quantum concept.
Quantum fluctuations
A more advanced concept of quantum mechanics is fluctuations, which stems from the Uncertainty Principle. As an example, think again of our one-electron atom. We have already said we can model the electron, which is not localised in space, but spread out within a cloud – a probability distribution. The probability implies if you look for the electron at a specific location multiple times, you will only find it some of the times when the distribution fluctuates and localises the electron where you are looking. We can apply this idea to the Dirac model pictured in Fig. 2.
Consider a system prepared such that there are no electrons in the positive states. We remember that the negative-energy states are filled with virtual electrons – the Dirac picture. There are no detectable electrons in the system at preparation. When we apply the uncertainty principle to this system, we let energy be one observable and time the other. Now we let the uncertainty in our knowledge of the energy be the energy gap between the top of the negative-energy states and the bottom of the positive-energy states (i.e., twice the electron rest-mass energy).
We calculate the minimum uncertainty in the time to be about 0.6 zeptoseconds, where 1 zeptosecond is 1 millionth of a femtosecond. This is the amount of time that the electron-hole pair can exist without violating the Uncertainty Principle. The fluctuations enabling virtual electrons to exist in the positive-energy states as real electrons momentarily are spontaneous and occur randomly.
Unification of electrodynamics, quantum mechanics and special relativity
Physicists are attracted to mathematical elegance in a theory. By that, I mean a theory should have a small number of parameters to explain phenomena and be predictive.
In addition, there is a desire for a theory to connect and explain more than one phenomenon. As a general goal, physicists seek the unification of theories and forces, if possible, into a single theory. Classical Electrodynamics is an example. It unified electric and magnetic forces, which were originally believed to be independent phenomena.
Their unification led to four basic equations – Maxwell Equations (due to John Clerk Maxwell) – that succinctly explain all of classical electrodynamics. That unification ushered in new insights, such as moving charges generating magnetic fields and oscillating electric fields generating oscillating magnetic fields, as well as a coherent description of light waves.
With the advent of quantum mechanics and relativity in the early part of the 20th century, there was a push for a unification of these two with electrodynamics. It turns out that Classical Electrodynamics already included special relativity, so only quantum mechanics was required to be included. That unification produced quantum electrodynamics (QED), one of the most successful theories in physics.
However, nearly all of the laboratory tests involving laser light have been in the weak-field, low-intensity limit, i.e., mostly in the two lowest regimes in Fig. 1. Petawatt lasers give us the ability to investigate QED in the strong-field limit.
That is, we are interested in processes and phenomena where the QED description of the physics involves additional expressions that are nonlinear in the light intensity. Because of the nonlinear expressions, we call this nonlinear QED. Petawatt lasers are ideally suited to investigate this new area of light-matter interaction as current lasers can reach intensities just under the threshold to the vacuum response regime and are slated to exceed that threshold in the not-too-distant future.
Stimulating and exploring the quantum vacuum
Now we have all the ingredients we need to outline two experimental goals for the top two regimes of Fig. 1. First, we need to define the quantum vacuum. We start by considering an ordinary vacuum. One generally thinks of a vacuum as being empty space, the essence of nothing. We can define a classical vacuum as having no matter (particles), specifically zero molecules per cubic centimetre, which, by the way, is actually very difficult to achieve. The best contemporary vacuums in the lab typically range from a few hundred to a few thousand molecules per cubic centimetre, with heroic efforts pushing these numbers down further, but not quite to zero. Nevertheless, we will take 0 molecules per cubic centimetre as our definition of a classical or ordinary vacuum.
Our definition of a quantum vacuum will be a bit different. We will define it as the lowest energy state – no real matter (again, 0 particles per cubic centimetre) and no energy sources. Because of fluctuations, the lowest-energy quantum state has what is called zero-point energy.
This energy, however, is not extractable. We also must consider the virtual particles in the Dirac Sea as they participate in the zero-point energy fluctuations. So, our quantum vacuum has no real particles but is filled with virtual particles. We learned that virtual electrons spontaneously become real, along with a corresponding hole that Dirac interpreted as a positron, for a very short period of time.
Consequently, zero-point energy fluctuations produce ephemeral electron-positron pairs. This will happen everywhere, generating a collection of randomly oriented pairs, as shown in the upper panel of Fig. 3. Our quantum vacuum has no real (long-lived) particles and no energy sources but is replete with ephemeral electron-positron pairs.
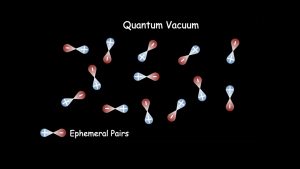
The experimental goal for the vacuum response regime is to detect and perhaps manipulate the ephemeral pairs. An experimental study of the quantum vacuum was first suggested by O. Halpern in 1933. Halpern’s proposal was to use two beams and look for light-light scattering. Maxwell Equations do not allow light-light scattering. Its observation would be a purely quantum mechanical effect and is allowed by nonlinear QED. It has never been observed in any region of the spectrum. Fig. 1 shows the approximate intensity threshold for the process to be observed. It is at least one order of magnitude beyond the intensity that has been achieved in the laboratory to date.
The theoretical foundation supporting light-light scattering was reported in 1936 by Heisenberg and his student Hans Heinrich Euler. They calculated the strength of the interaction between two beams with their oscillating electric fields aligned and perpendicular to each other. Their calculations showed that the interaction is significantly stronger when the fields are perpendicular to each other. While their work was prior to the full development of QED, it is incorporated in the current version of QED.
Quantum electrodynamics offers a model for what is happening during light-vacuum interaction. The ephemeral pairs will act like little electric dipoles.14 A classic undergraduate physics problem is to calculate the response of a dipole placed in a static electric field. The solution is the positive charge feels a force pushing it in the direction that the electric field points, while the negative charge is pushed in the opposite direction. The axis of the dipole will quickly align itself with the field.
A laser field is a bit more complicated because the direction of the electric field (as well as the magnetic field) oscillates at a high frequency, first pointing in one direction and then in the opposite direction. This is not a problem for these pairs because the mass of electrons (as well as positrons, which have the same mass) is so small that they can follow the field oscillation. The net result is an orientation of the pairs with the electric field direction of the laser pulse.
The lower panel of Fig. 3 shows an artist’s rendition of a snapshot of the orientation when the pump laser’s electric field points up. The panel also shows two probes interacting with the oriented pairs, one at a time. Again, when the fields of the pump and probe lasers are perpendicular to each other, the interaction is stronger.
However, the effect is extremely small, which is why the intensity must be so high to observe the effect. It is interesting to point out that when the laser interacts with the ephemeral pairs, the speed with which it travels through the vacuum is slowed ever so slightly. Because of the interaction when the electric field of the pump (orienting the pairs) and that of the probe are aligned or perpendicular, the probe will travel at two different speeds. That is, the light speed will have one value when the electric field of the probe is aligned with the pairs and a different speed when it is perpendicular to the pairs. This effect has not been observed in the lab but may contribute to understanding dynamics in astrophysical systems where super-intense magnetic fields cause a similar effect.
To test QED, there are experimental plans to measure the strength of the interaction in both cases displayed in Fig. 3. If the experimental results differ from theoretical predictions, this could be evidence for new physics. It has been reported for some time that the bulk of the energy in the universe is unknown. Some of this energy appears to be wrapped up in unseen matter. I say unseen because it apparently does not interact with electromagnetic waves, or if it does it is so weak it is imperceptible with current; hence the name Dark Matter This is where a study of the quantum vacuum comes in.
There are several theories that suggest that certain types of proposed dark matter candidates, called axions, may cause measurement results to be shifted away from the QED prediction. While the petawatt-based quantum vacuum experiments are being designed to measure the QED prediction, observing interaction with dark matter might be an added bonus.
There are several facilities building new lasers that should be in range to perform such an experiment within the foreseeable future. In addition, there are several possible approaches to realising experiments to see the oriented pair depicted in the lower panel in Fig. 3. A number of experimental teams around the world are pursuing such an experiment, including ours at the University of Maryland, supported by the U.S. National Science Foundation and the US Department of Energy.
Teasing real electron-positron pairs out of the quantum vacuum
The top regime, the vacuum breakdown regime, is, as the name implies, where there is sufficient intensity in the laser field to separate the electron from the positron before quantum fluctuations returns the ephemeral pair back to its virtual state. The threshold for this pair production is shown in Fig. 1 as well. This is considered the holy grail by some in the laser plasma community. We are a long way away from being able to reach this threshold with just laser pulses alone.
However, there are interesting suggestions under investigation that would allow investigators to bootstrap their way up to the threshold. We point out that to date, there has been only one laser-based experiment in this realm performed in 1999 at SLAC National Accelerator Laboratory.
There are a handful of experiments tooling up to repeat that experiment with higher-powered lasers. Why is this so interesting, you may ask? Pair production is one of the fundamental processes predicted by relativistic quantum mechanics.
More importantly, using lasers to induce pair production may be the cleanest way to generate an electron-positron pair plasma, which many suspect is fundamental to a number of astrophysical systems in the universe. Some examples include black holes, pulsars and active galactic nuclei.
These entities contain a tremendous amount of energy and produce a variety of spectacular events such as gamma-ray bursts, relativistic winds and extremely intense magnetic fields, evidenced by stunning images captured by the Hubble and James Webb space telescopes as well as ground-based instruments.
At the moment, these systems and features can only be observed from afar. Scientific advancement, however, requires controlled experiments in which repeated measurements are made and various conditions adjusted judiciously.
While it does not seem likely that we will have the capability to reproduce a full suite of conditions for any of these systems in the laboratory in the near term, the advent of multi-petawatt lasers has brought us a step closer to being able to realise this ultimate plasma – the pair plasma.
Conclusion
This brings us to the end of this article, but not the end of the story. The story is still unfolding as researchers around the globe are working diligently to realise experiments with the quantum vacuum as their target. I hope you enjoyed the journey. I would like to end with three thoughts.
First, we have seen the importance of models and how they can help to guide our thinking. However, one must remember that models are just that; they can only take us so far, and then one must sit down and do the hard work of detailed theory.
Second, I would be remiss not to mention that, as we saw with rays, models do not always represent the whole story. There is a more correct way to view QED and the quantum vacuum than with the virtual-particle, ephemeral-pair model. The modern theoretical way to view the problem is through the lens of Quantum Field Theory (QFT); QFT treats the quantum vacuum as a field where virtual particles and ephemeral pairs are fluctuations in the field. One can make quantitative predictions of interaction strengths and other details with QFT. One would be hard-pressed to make quantitative predictions with the models that got us to this point.
Nevertheless, models are essential to enable us to picture and sketch experimental concepts. Theory is indispensable to get to the design stage and critical for analysis and interpretation. Finally, we end as we began, relying on light to continue to illuminate our path to scientific truths. Stay tuned for the next chapter.
References
- The corpuscular idea of light dates back to ancient philosophers. Today, we refer to a quanta – a package – of light as a photon.
- The wave nature was clearly demonstrated in 1801 by light interference leading to bright (constructive interference) and dark (destructive interference) fringes when light passed through two closely spaced narrow slits.
- The removal of electrons from matter depends on the wavelength (energy) and not the intensity.
- Radiation emitted by matter that depends only on its temperature. A correct description fitting the experimental observation is only possible by invoking Planck’s quantised radiation law.
- The only way an electron will move in a circle is if it is experiencing a force. Otherwise, it would move in a straight line according to Mr. Newton’s First Law of Motion.
- It is important to understand that Hamilton’s Principle is just a restatement of Newton’s Laws, albeit more versatile.
- Louis de Broglie had a similar thought and pondered the connection between matter trajectories and the wave nature of matter.
- He gave credit to Born, Jordan and Dirac for developing some of the ideas he used.
- A Watt is a measure of power or energy per unit of time.
- When the electron’s speed is less than 1% of the speed of light, the magnetic force can generally be neglected.
- We have invoked Einstein’s mass-energy equivalence — mass is just a different form of energy.
- Sometimes, an electron bound in an atom is said to have negative energy. In the Dirac case even the rest-mass energy is negative! Rest mass does not appear in the Schrödinger Equation.
- The Pauli Exclusion Principle implies that no two electrons can occupy the same state at the same time.
- A dipole is a bound pair of charges, one being positive (the positron) and the other being negative (the electron).
Please note, this article will also appear in the 22nd edition of our quarterly publication.









