Studying neutron star matter in the laboratory

Goethe University’s Professor Joachim Stroth explores neutron star matter and what happens when two of the densest macroscopic objects we know of merge.

What happens when two of the densest macroscopic objects we know of merge? Incredible amounts of kinetic energy are converted to heat and bring neutron star matter to temperatures so high that a transition to exotic phases might be possible. A world-wide research programme aims at unravelling the microscopic properties of such states of matter. Compressed baryonic matter is recreated in the laboratory in tiny portions but large enough to reveal macroscopic properties in collisions of heavy ions at relativistic energies. There are hints that the building blocks of matter, the nucleons, start to melt and form a new state characterised by a soft deconfinement.

Among the most fascinating astrophysical events are the encounters of massive compact stellar objects. In October 2017, the ninth gravitational wave signal was detected, but this time with a frequency pattern very distinct from the ones observed before. While so far the signals could be explained as originating from two black holes merging into a single one, the observation of GW170817 found a sound interpretation by assuming a merger of two neutron stars.¹ Such remnants of dead stars are very compact. They feature diameters below 30 km but exhibit masses of one to two times the solar mass. Consequently, its constituents, dominantly neutrons, are squeezed beyond the level to which nucleons are packed in atomic nuclei. This fact makes these objects equally interesting for astrophysicists as well as for nuclear physicists.

Binary neutron star mergers

What makes the difference of GW170871 to all observed merger events before is the fact that the combined mass of the binary system was small enough that the remaining object still survived as a neutron star, albeit with much reduced mass. As a result, a substantial fraction of the matter was ejected into the interstellar space during the merger process. The properties of this ejecta and the ambient conditions were such that rapid neutron capture processes occurred and nuclear synthesis took place. It is assumed that in such events gold in an amount of ten times the mass of the earth can be produced, besides many other heavy elements, and dispensed into the interstellar space.²

This conjecture found major support by the observation of related electromagnetic radiation in a wide spectral range, originating from the same region and detected in coincidence with the gravitational wave signal.³ Since then, neutron star merges of this type are now considered to be the major cosmological site of element synthesis.

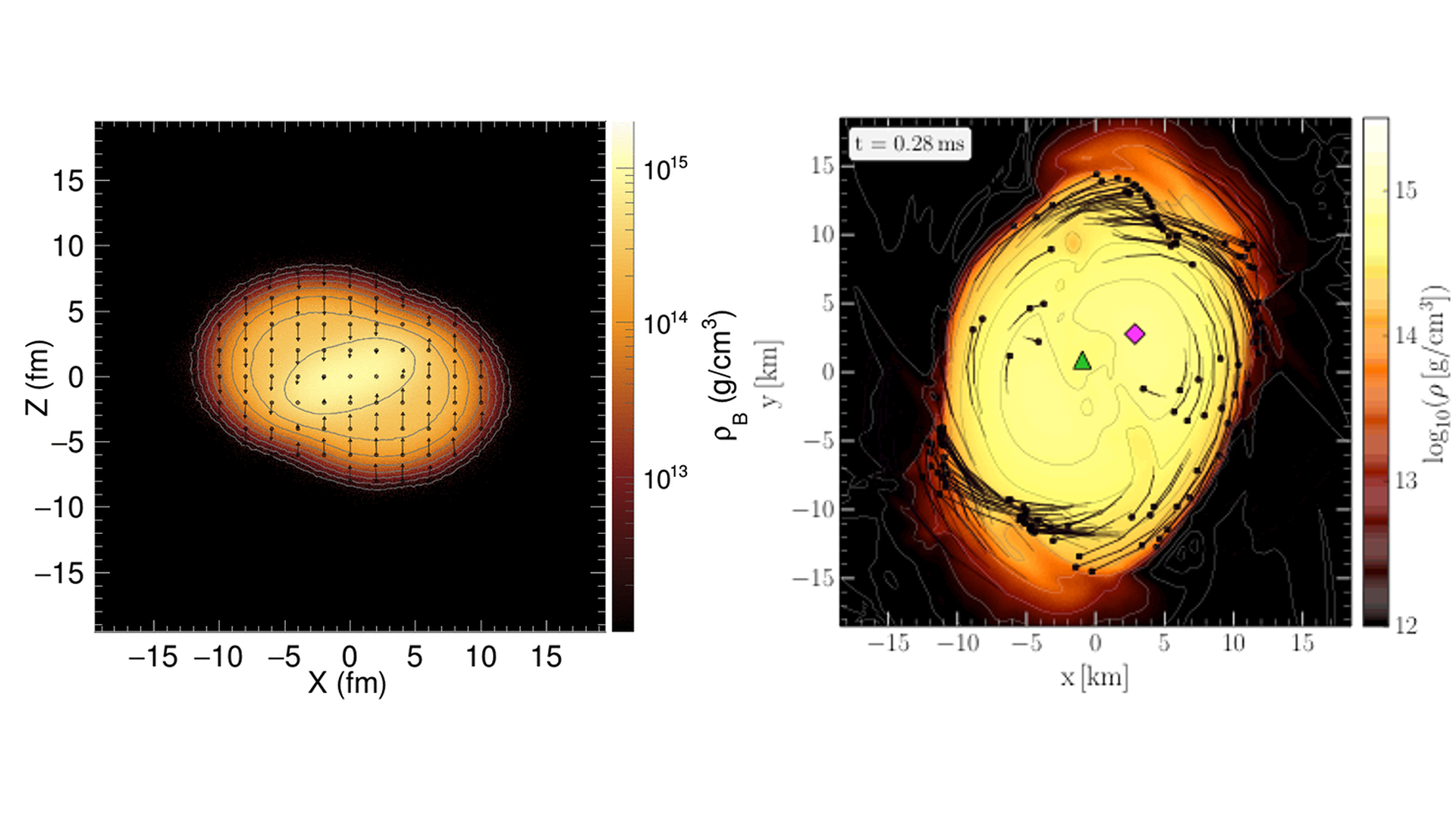
But let us turn back to the core of the merging binary system. Obviously, the remaining neutron star must have undergone a violent transformation during which the dense matter was heated to extremely high temperatures. There is a longstanding debate around whether, under such extreme conditions, strong-interaction matter – that is, any form of matter made up of elementary (quarks) or composite particles thereof (hadrons) and all governed by the strong interaction – would undergo a phase transition into a novel phase of matter.²

We have very strong evidence that one such exotic state of matter filled the whole Universe about 10 μs after the Big Bang. At this time, the elementary building blocks of hadrons, the quarks and gluons, were still roaming freely and existing in a phase called the Quark Gluon Plasma (QGP). Once the temperature dropped, this phase changed to isolated droplets which became the hadrons in many different states of excitation. Today, protons survive as the only stable hadron, and neutrons are bound to protons, thus forming atomic nuclei.

The extreme conditions prevailing when protons and neutrons were created still exist in the core of nucleons. While in an atomic nucleus, nucleons do not come close enough such that the cores of the nucleons would overlap, the high pressure and temperature created in neutron star merger processes could change this situation.

The nucleon as building block of matter

To better understand the microscopic structure of neutron star matter, or particularly the matter formed in the merger of two of them, it is reasonable to have a closer look to the structure of the nucleon. The quantum numbers of the nucleon like their electric charge or spin are determined by three valence quarks. They are bound tightly together by the strong force, which is mediated by the exchange of gluons. While on the one hand nature tries to minimise the cost of this interaction by bringing the elementary particles as close together as possible, quantum mechanics on the other hand allows such a localisation (Δx) only at the expense that the particles gain large momenta (Δp). That latter phenomenon has been cast by Heisenberg into the formulation of the Uncertainty Principe: Δx Δp > ħ/2.

The result of this balancing process is the bound state and a mass of this state, about a hundred times larger than the mass of the three valence quarks. The large momenta of the valence quarks give rise to abundant vacuum excitations which manifest as virtual quark-antiquark pairs and which add to the structure of the nucleon. Moreover, because of the strong coupling and self-interaction of the force mediators, the nucleons also contain many gluons. Consequently, the nucleon is a very dynamic object and the reason why it has preserved the high temperature of the early Universe at the time the nucleons were formed out of the QGP. It also demonstrates the utmost importance of the two major discoveries in physics of the early 20th century, namely special relativity (mass-energy equivalence) and quantum mechanics (the Uncertainty Principle).

The important take home message of this short discussion is the perception that the nucleon mass is almost entirely due to dynamics generated by the strong force and that the nucleons do not have a well-defined surface. Rather, the surface is determined by the distance the virtual excitation of quark-antiquark pairs are able to separate from the nucleon core as dictated by the Uncertainty Principle.

How can deconfinement occur in dense baryonic matter?

We know that the QGP of the early Universe can be recreated in the laboratory by colliding heavy ions at ultra-relativistic energies.⁴ That is, at kinetic energies a hundred to a thousand times higher than the mass of the colliding objects. Many results of experiments carried out at the RHIC or LHC hadron colliders have demonstrated the creation of deconfined matter. In this case, QGP is produced in the collision zone by abundant gluon-gluon interactions, while the constituent quarks essentially leave the interaction zone rapidly. But is there a way to de-confine the nucleons by other means? Thorough theoretical studies are underway to investigate under which conditions strong-interaction matter could exist in a deconfined state in neutron stars or would undergo a phase transition into a novel phase of matter during binary merger events.

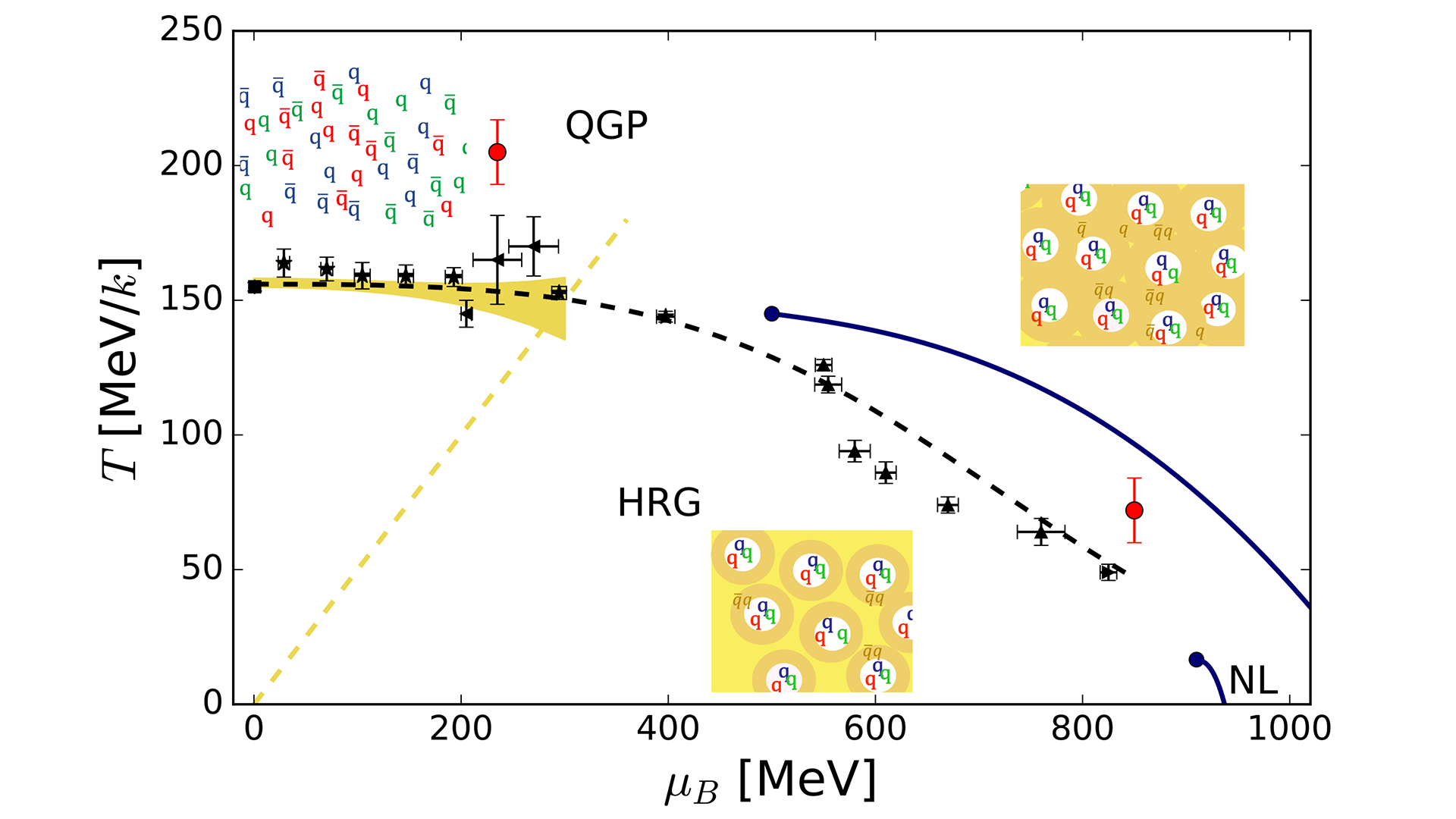
The nature of the strong interaction, however, prevents calculations based on first principles. At GSI, the Helmholtz Research Center for Heavy-ion Research in Germany, a long-term research programme is dedicated to the exploration of the microscopic properties of dense, or compressed, baryonic matter using central collisions of relativistic heavy ions. It is commonly accepted that in collision at beam energies of a few times the nucleon mass, in contrast to the case at ultra-relativistic collision energy, the incoming protons and neutrons are stopped in the collision zone and dynamically compressed to form baryon-dense matter. Inertia works against the hard-core repulsion of the nucleons. In the interior of a neutron star, this compression is realised by the immense gravitational force.

There are two more remarkable differences: in a heavy-ion collision, matter is substantially heated up due to friction, while a neutron star is never really hot and has cooled down since the time of its formation. In merger processes, though, that situation is expected to change as the relative motion of the two encounters generates tremendous friction. A second difference is the composition in terms of electric charge. While neutron stars are electrically neutral as electron capture processes have converted most of the protons to neutrons, the matter created in heavy-ion reactions has a positive charge surplus because of the protons in the nuclei while the electrons have been stripped off.

To develop an insight into the structure of hot compressed matter we will shift the focus on the role of the virtual quark-antiquark excitations characterising the nucleon. The interaction between nucleons coming close to each other is understood to occur because of the overlap of the diffuse surfaces of the nucleons. This leads to the exchange of virtual quark-antiquark excitations and by this to a momentum and energy transfer.

Quark-antiquark states can form mesons, and the lightest of such mesons is the pion. The range of this meson exchange force can be estimated on the basis of the rest mass of the meson. According to the uncertainty relation, energy conservation can be violated on a time scale inversely proportional to the amount of energy violation. A pion formed out of the vacuum (virtual state) can exist long enough to separate from the nucleon core by about 1.5 fm, roughly the distance at which two nucleons exist inside an atomic nucleus.

In the language of quantum mechanics, the wave functions of these virtual meson excitations of neighbouring nucleons are ‘entangled’. In the case, the average inter-nucleon distance is reduced because of compression, such an entanglement can extend over larger regions and involve more than just two nucleons. If at the same time the temperature of the matter reaches values representing a substantial fraction of the pions mass, the extension of the meson cloud is increased further as this ‘energy reservoir’ can be used to bring the pions nearer to the mass shell (virtuality is partially lifted). Such a form of matter would be characterised by an extended entangled meson cloud in which the nucleon cores are embedded.

Fig. 2 depicts the location of different conjectured phases in a sketch of the phase diagram of strong interaction matter. A full theoretical description of such a form of matter, on the basis of the elementary building blocks, is not possible since strong interaction prevents the use of perturbation theory. First attempts to model such a state have found that quarks could indeed roam over larger distances and a soft deconfinement would occur.⁵

Searching for signatures of soft deconfinement

There are two promising observables investigated in relativistic heavy-ion collisions which have the potential to shed light on the structure of the phase realised under these conditions. Along with the entanglement of the baryonic meson clouds, the properties of hadrons in general are expected to substantially change inside the dense and hot medium. An observable factor directly connected to such in-medium modifications is electromagnetic radiation. Photons couple to hadronic states dominantly via intermediary vector mesons. Such mesons do not carry electric charge and have also otherwise the same quantum numbers as the photon. Of particular interest are virtual photons, which are detected via their decay into a pair of electrons (𝑒⁺𝑒^–) or muons (µ⁺µ^–).

From the spectral distribution of such lepton pairs, the invariant mass distribution can be reconstructed. This is a direct measure of the in-medium spectral function of the vector meson.⁶ A first series of such measurement has recently been published by the HADES collaboration evidencing a strong melting of the vector mesons in medium.⁷ A rapid thermalisation of the excitation spectrum of the hadrons could be a second signature of an entanglement of the meson clouds. It is well known that the excitation energy of a baryon can also be carried by the meson cloud and not only by a reconfiguration of its valence quarks. Indeed, model calculations of excited baryon states show that the respective wave function can contain components characteristic for a bound meson baryon state. This theoretical result is supported by measurements of the baryon structure using electron scattering and by first measurements of dilepton decays of baryonic resonances, carried out by HADES.

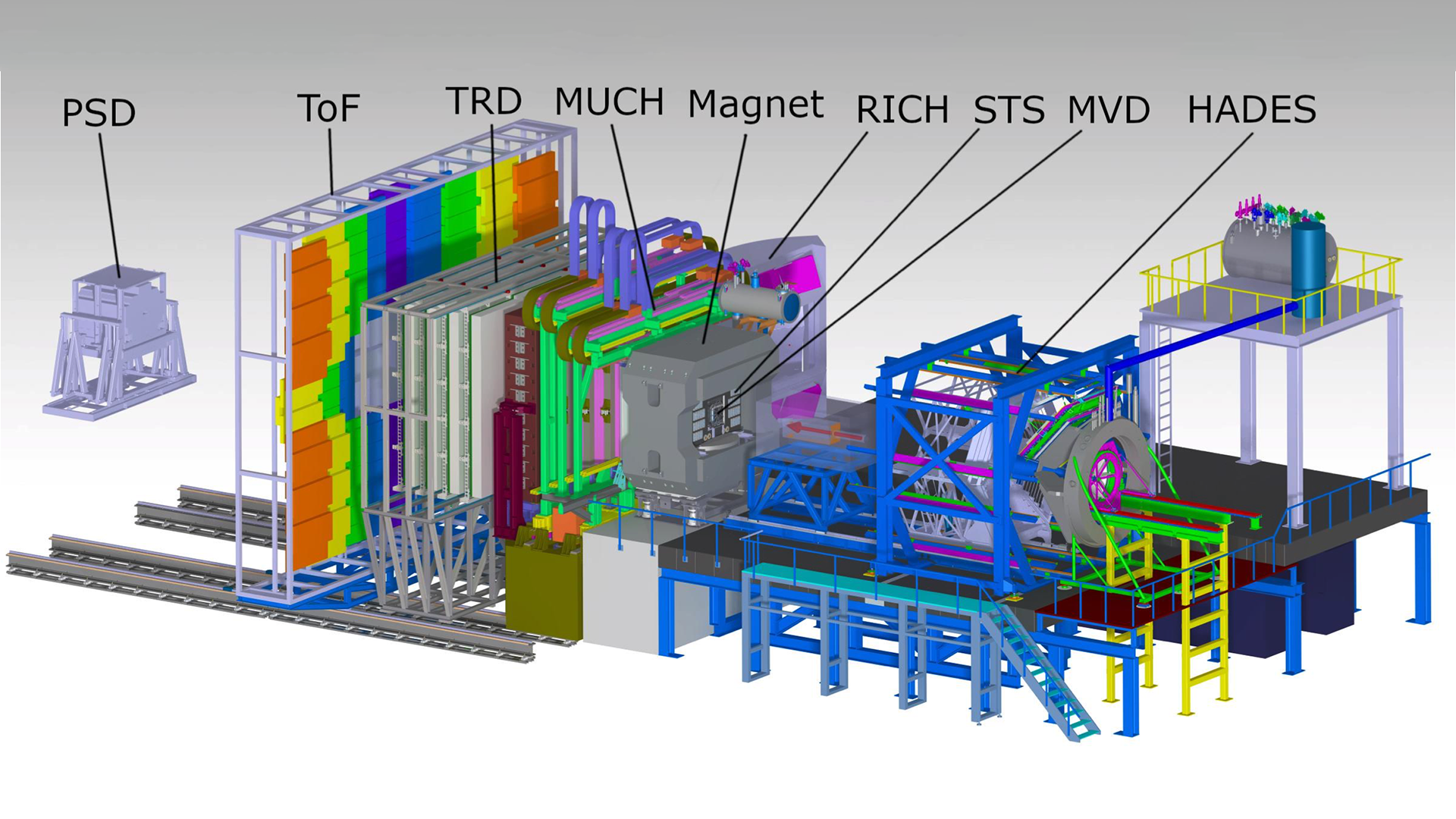
Compressed baryonic matter research at the FAIR facility

At the site of GSI, the new international Facility for Anti-proton and Ion Research (FAIR) is currently being constructed. FAIR represents one of the largest investments in fundamental research in recent years and is dedicated to the study of the formation of matter on almost all scales, from the elementary quarks, to hadrons, to strong-interaction matter, and also various aspects of atomic, plasma, and material science. For the investigation of compressed baryonic matter a new, dedicated experiment is currently constructed which will substantially go beyond the capabilities of HADES.⁸

Fig. 3 shows computer graphics of the two experiments located in one of the experimental caves of FAIR. The CBM experiment will enable studies of heavy-ion collisions at interaction rates of several MHz to gain sensitivity in particular to the rare and electromagnetic probes of extreme states of matter.⁸ To accomplish this formidable task, the detector systems, indeed any single detector cell, will independently send information about impinging particles to a central compute farm. This will generate a data stream of TB/s which will contain plenty of information about the reactions taking place. Fast, highly parallel algorithms will provide event reconstruction in real time, employing in parallel up to 40,000 processor cores. The German Ministry of Education and Research (BMBF) supports this programme in the framework of ErUM FSP 107 C.B.M, dedicated in particular to university groups. Additional support, also involving theoretical activities, is provided by the Helmholtz Research Academy of Hessen for FAIR (HFHF). Embedded in FAIR, the CBM experiment is operated by an international collaboration including scientists from numerous countries. GSI acts as a host laboratory for the international collaborations and is a member of the Helmholtz Association of German Research Centers e.V. (HGF).

Acknowledgements

This work was support by HFHF and ErUM FSP C.B.M. We also thank Peter Senger for his careful reading of the manuscript.

References

1. P. Abbott et al. GW170817: ‘Observation of Gravitational Waves from a Binary Neutron Star Inspiral’. Phys. Rev. Lett., 119(16):161101, 2017
2. Andreas Bauswein, Niels-Uwe F. Bastian, David B. Blaschke, Katerina Chatziioannou, James A. Clark, Tobias Fischer, and Micaela Oertel. ‘Identifying a first-order phase transition in neutron star mergers through gravitational waves’. Rev. Lett., 122(6). 061102, 2019
3. P. Abbott et al. ‘Multi-messenger Observations of a Binary Neutron Star Merger’. Astrophys. J. Lett., 848(2). L12, 2017
4. Anton Andronic, Peter Braun-Munzinger, Krzysztof Redlich, and Johanna Stachel. ‘Decoding the phase structure of QCD via particle production at high energy’. Nature, 561(7723). 321330, 2018
5. Kenji Fukushima, Toru Kojo, and Wolfram Weise. ‘Hard-core deconfinement and soft-surface delocalization from nuclear to quark matter’. Rev. D, 102(9). 096017, 2020
6. Piotr Salabura and Joachim Stroth. ‘Dilepton Radiation from Strongly In-teracting Systems’. Prog. Nucl. Part. Phys., 5 2020
7. Adamczewski-Musch et al. ‘Probing dense baryon-rich matter with virtual photons’. Nature Phys., 15(10):1040-1045, 2019
8. Bengt Friman, Claudia Hohne, Jorn Knoll, Stefan Leupold, Jorgen Randrup, Ralf Rapp, and Peter Senger (editors). The CBM physics book: Compressed baryonic matter in laboratory experiments, Volume 814. Springer, 2011
9. L. Rezzolla et al. Phys. Rev. Lett. 122, 061101 (2019)