Theoretical particle physicists are providing exact predictions to compare LHC measurements to reveal the strengths and shortcomings of the Standard Model.
Discoveries behind the decimal point
A quantum theory called the Standard Model describes the world of known elementary particles and their interactions. However, the nature of Dark Matter and why matter is abundant over anti-matter in the Universe are examples of questions the Standard Model does not answer. New particles or interactions are expected to exist that would provide such an explanation.
The Large Hadron Collider at CERN, the world’s most powerful particle accelerator, may produce new physics particles, but none have been detected at this stage. Therefore, the community is engaged in a more indirect approach.
This indirect approach directly leverages the quantum mechanical nature of elementary particle physics. Even if new particles are too heavy or too weakly coupled to be produced in sufficient numbers to stand out above the background, they can subtly change other reactions so that these do not entirely conform to the SM expectations.
Thus, it is in such minor deviations that possible discoveries may well be found. It is clear that for this to succeed, both measurements and theoretical calculations must be precise, with the smallest possible uncertainty margins. The experiments on the Standard Model are impressively meeting this challenge, thanks to an increasing data set and better, innovative analysis methods.
The high-order perturbation theory
To test the Standard Model, the theoretical particle physics community has started to develop and use methods for highly precise calculations. Theorists use mostly a perturbative approach based on Feynman diagrams.
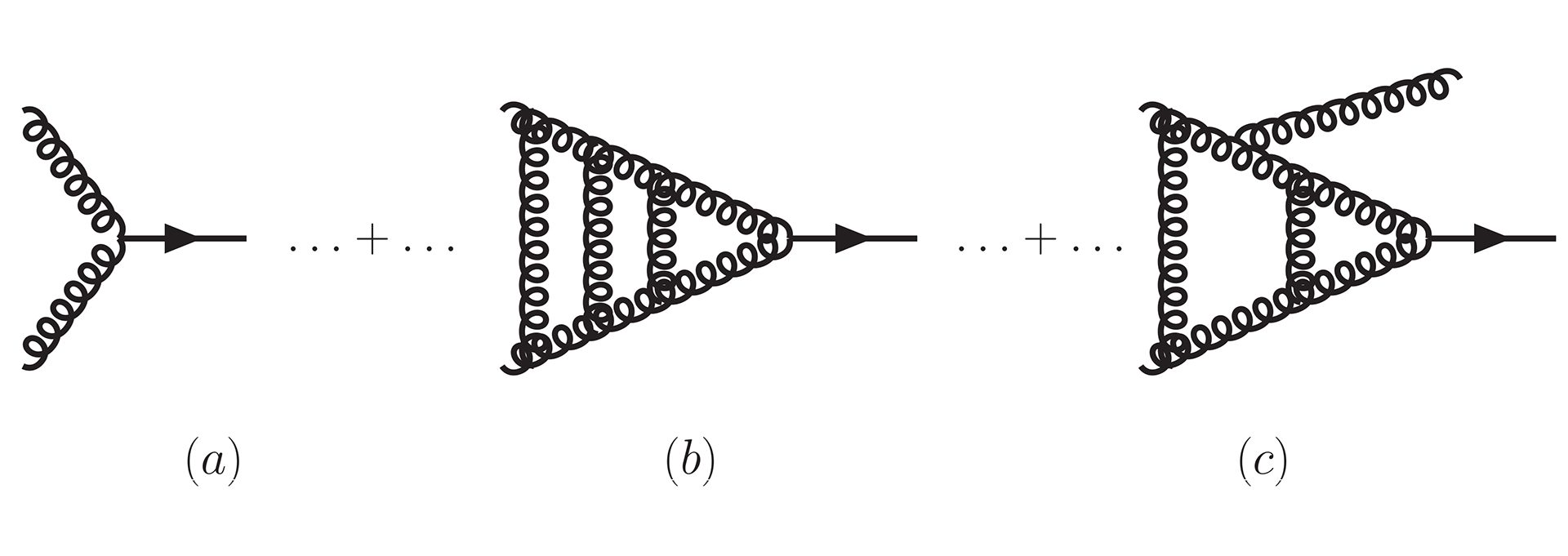
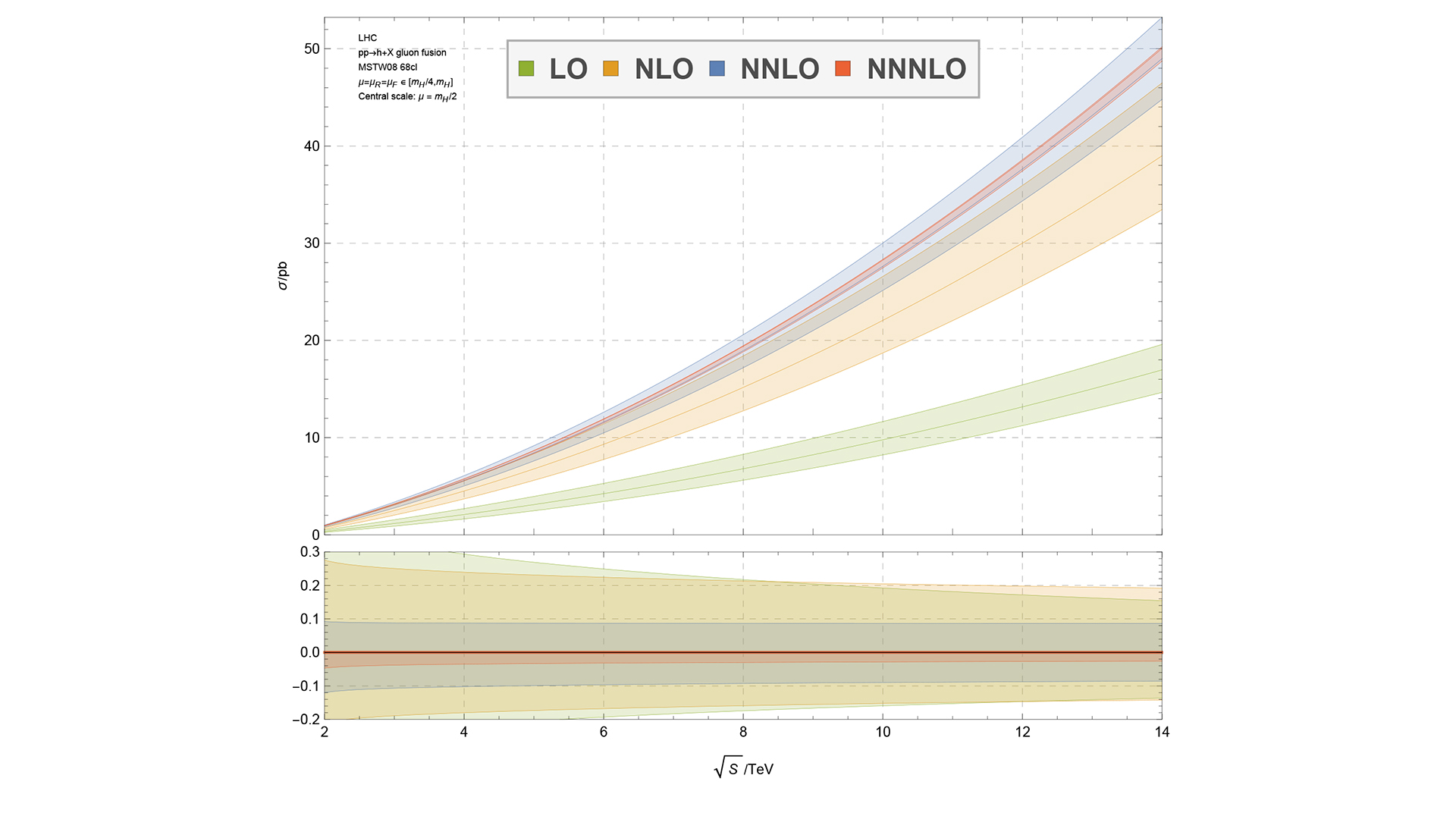
More precision means calculating diagrams with more loops and radiated particles (Fig. 1). This presents an enormous challenge. Not only do graphs with more circles become much more difficult to compute, but their number also increases dramatically. For instance, for the third-order correction to the Higgs boson production rate, calculated by a group primarily based in Zurich (and Amsterdam)1, the lowest order consists of one simple diagram. The number reaches well into the millions at the third order. The result leads to a much smaller uncertainty (Fig. 2).
Computer algebra with FORM
This endeavour can only exist with extensive use of high-performance computing. For the aforementioned third-order correction, 25,000 cores were engaged for two months. A vital role is played by symbolic computer algebra. The well-known programmes, Mathematica and Maple, are not built to handle the extreme needs of such calculations.
At Nikhef in Amsterdam, Dr Jos Vermaseren developed the FORM open-source computer algebra programme2 to test the Standard Model, which can deal with such conditions thanks to its highly tuned and innovative algorithms and efficient programming. The continued development and long-term support of FORM is now a significant concern3, and while efforts are underway to ameliorate this situation, active contribution to its development is welcome.
Amsterdam theoretical particle physics
Computer software and hardware are not the only ingredients needed to provide precise theoretical predictions for the LHC physics programme. As recognised by the European Strategy for Particle Physics update in 2020:4 “Both exploratory research and theoretical research with direct impact on experiments should be supported, including recognition for the activity of providing and developing computational tools.”
Thus support for theorists and theory groups that engage in such long-sustained efforts is also needed. The Free University of Amsterdam, the University of Amsterdam, and the neighbouring Nikhef National Institute for Subatomic Physics in the Netherlands have supported such efforts for many years. Together, they form a unique ecosystem in Amsterdam, not just due to their mutual proximity, but the seamless way collaboration happens. In particular, Nikhef is an international cooperation model, shaping particle physics research at six universities and the NWO funding agency.
Besides being the home of FORM, through the work of Professor Juan Rojo, Amsterdam is a significant node of the Neural Network Parton Distribution Function collaboration (NNPDF), which produces sophisticated initial conditions for the theoretical calculations required for the LHC.
In addition, there are strong efforts by Drs Wouter Waalewijn, Jordy de Vries, Melissa van Beekveld and the author in fixed higher-order analyses, all-order approaches to providing predictions, and Parton shower improvements for both high and low-energy scattering observables aided by effective theory frameworks.
Observables, where the bottom quark plays a key role, are particularly interesting in searching for indirect signs of new physics. In such studies, the violation of CP invariance (the combination of charge conjugation C and parity transformation P) can occur, which is intimately linked to matter over the anti-matter abundance question. Professor Robert Fleischer is studying how to tease new physics signals from the data. But not only in collider data are minor deviations interesting. Professor Marieke Postma, also at Nikhef, studies how to tease subtle signs of new physics from early Universe observations, when conditions were even more extreme.
New methods for testing the Standard Model
It may be interesting to highlight a few recent innovations in computational methods that have allowed the field to achieve the significant advances it has made towards precise calculations about the Standard Model.
Many of these are associated with complicated integrals, which must be carried out when computing Feynman diagrams with loops (Fig. 1b) or extra emitted particles (Fig. 1c). Many relations between the loop integrals can be established, using tricks as relatively straightforward as integration-by-parts. These relations imply that a much smaller set (the ‘master integrals’) needs to be calculated, from which all others follow. For calculating these master integrals, powerful new techniques now exist, such as using differential equations or a map to a multi-dimensional dimensional complex integral where Cauchy’s theorem comes into practice.
These new methods are now encoded into software packages, often in Mathematica, so a modern theorist rather than being depicted as sitting with a pencil and paper. It is more likely to be weaving together symbolic results in software. A particular emphasis in Amsterdam is calculating the largest terms in any order and then summing these terms, an effort known as resummation. This is a complementary approach to the order-by-order approach and helps further reduce the uncertainty of predictions.
The huge LHC dataset yet to come will provide many more and stricter precision challenges to theorists. We look forward to meeting this challenge in Amsterdam and the community at large. After all, it may lead to spectacular discoveries about the Standard Model.
References
- “Higgs Boson Gluon-Fusion Production in QCD at Three Loops”, C. Anastasiou, C. Duhr, F. Dulat, F. Herzog, B. Mistlberger, Rev.Lett. 114 (2015) 212001
- Kuipers, T. Ueda, J.A.M. Vermaseren and J. Vollinga, Comput. Phys. Commun. 184 (2013) 1453; B. Ruijl, T. Ueda and J. Vermaseren, arXiv:1707.06453
- “Crucial Computer Program for Particle Physics at Risk of Obsolescence”, M. von Hippel, Quanta Magazine, Dec. 1, 2022
- https://europeanstrategy.cern/







