Important developments in theoretical nuclear physics and understanding the fine-tuning of the Universe that has led to the evolution of life on Earth.
Element generation in the Big Bang and in stars exhibits fine-tuning that is of utmost importance for the formation of life on Earth. Using modern theoretical tools like effective field theories and Monte Carlo simulations allows us to find out how much detuning of the fundamental parameters of the Standard Model is permitted for viable life on Earth.
Theoretical nuclear physics has undergone remarkable changes in the last two decades. With the development of effective field theories (EFTs) to calculate the forces between nucleons and improved many-body methods such as nuclear lattice EFT, nuclear structure observables and astrophysical reactions can now be calculated from first principles with superb accuracy and quantifiable uncertainties.
Furthermore, these methods allow scientists to consider different values of the fundamental parameters relevant to nuclear physics, namely variations of the light quark masses mu and md and the electromagnetic fine-structure constant αEM. Thus, we can indeed ask the question: How accidental is life on Earth? It also allows us to understand important concepts, like the limit of nuclear stability (the drip lines), or the phase diagram of nuclear matter, which can now be calculated in a systematic fashion and with unprecedented accuracy, shedding new light on the matter surrounding us, which is largely made of atomic nuclei.
Theoretical developments
As the field develops, theoretical nuclear physics has turned from a largely model-dependent to a well-defined, first principles framework. An important step was made by Nobel laureate Steven Weinberg in 1991, who extended the successful approach of chiral effective field theories (EFTs) to systems with two and more nucleons. EFTs have become a major tool in particle, nuclear and condensed matter physics, as they allow for precise and systematically improvable calculations of strongly interacting systems in a given energy regime. For the strong interaction, chiral symmetry and its spontaneous and explicit breaking is of utmost importance to set up the pertinent EFT, which is called chiral perturbation theory. Within the chiral nuclear EFT framework, consistent calculations of two- and three-nucleon forces, as well as of external currents are possible, including the fine effects of isospin-breaking. In the two-nucleon sector, such investigations provide the most accurate description of the large amount of proton-proton and neutron-proton scattering data, and these chiral forces are used worldwide combined with classical many-body approaches, such as the shell model or the coupled-cluster method.
A second important development is the stochastic (Monte Carlo) methods that use a discretized, finite-volume space-time amenable to high-performance computing to solve the nuclear few- and many-body problem exactly. This new approach is called nuclear lattice EFT. Not only does it allow for precise nuclear structure calculations, it also addresses reactions that were considered intractable before. As two prominent examples, the first ab initio and parameter-free calculations of the Hoyle state in 12C in 2011 and of low-energy 4He-4He scattering in 2015 should be mentioned.
Moreover, combining chiral EFTs with such lattice simulations allows us to consider different worlds that are characterised by different quark masses and electromagnetic interactions as we observe them. This can shed light on the anthropic view of the Universe, namely on how much fine-tuning is really involved in the processes that generate the elements relevant for life or stated differently: Is the Hoyle state really, as said by the Stanford physicist Andrei Linde, the “level of life”?
Precision calculations in nuclear physics
To answer the aforementioned questions, calculations at the (sub)percent level are mandatory. With physics beyond the Standard Model (BSM) becoming more and more elusive at high energy colliders like the LHC at CERN, low-energy precision experiments involving nuclei are gaining more importance in the search for BSM physics. Of course the Standard Model uncertainties have to be made smaller than the eventual BSM signal to make such investigations meaningful. Also, nuclei are used as targets for the scattering of Weakly Interacting Massive Particles (WIMPs), one of the prime candidates of the elusive dark matter, producing a very small but measurable recoil. This is done to worldwide in various experiments requiring good control of the nuclear structure uncertainties. Another example is neutrino-less double β-decay, which is measured in nuclei, allowing scientists to understand the precise nature of the neutrinos.
Fine-tunings in the Big Bang
The light elements up to 7Li were produced in the first few minutes after the Big Bang; the generation of the a-particle (the 4He nucleus) is of particular interest, as this together with the other light elements has been the basis of star formation during the later stages of the Universe. In order to investigate element generation, we must consider a network of nuclear reactions, in which the properties (masses, cross sections and so on) of all participating particles depend on the quark masses and on the fine-structure constant. The neutron lifetime is significant, as its value determines how many of the neutrons decay before they are finally captured in light nuclei, like the deuteron, 3He and 4He. Thus, the weak neutron decay plays an important role in generating the abundancies of the light nuclei that we observe today. Requiring that the element abundancies are similar to those measured in our Universe, sets stringent limits on the variation of the fundamental parameters. Assuming that the Yukawa couplings of the Higgs boson to the quark and fermions do not change, the deduced variation of the quark masses can be translated into a limit on the variation of the vacuum expectation value of the Higgs boson, which is the fundamental field generating the mass of all quarks and leptons. Indeed, this variation must be less than one percent to generate a sufficient amount of deuterium and α-particles.
It has also been theorised that the θ-theta term of QCD, that leads to strong CP-violation as measured (e.g. in nuclear electric dipole moments), is of natural size (of order one) in the early Universe rather than 10-10 as determined in the present Universe. While it has been found that the binding energies of the light nuclei are considerably altered when θ is of order one, Big Bang nucleosynthesis would proceed, producing more deuterium and less helium. Interestingly, the di-neutron and the di-proton become bound at θ ≅ 0.2 and θ ≅ 0.7, respectively, so hydrogen burning occurs at lower temperatures would cause stars to be different.
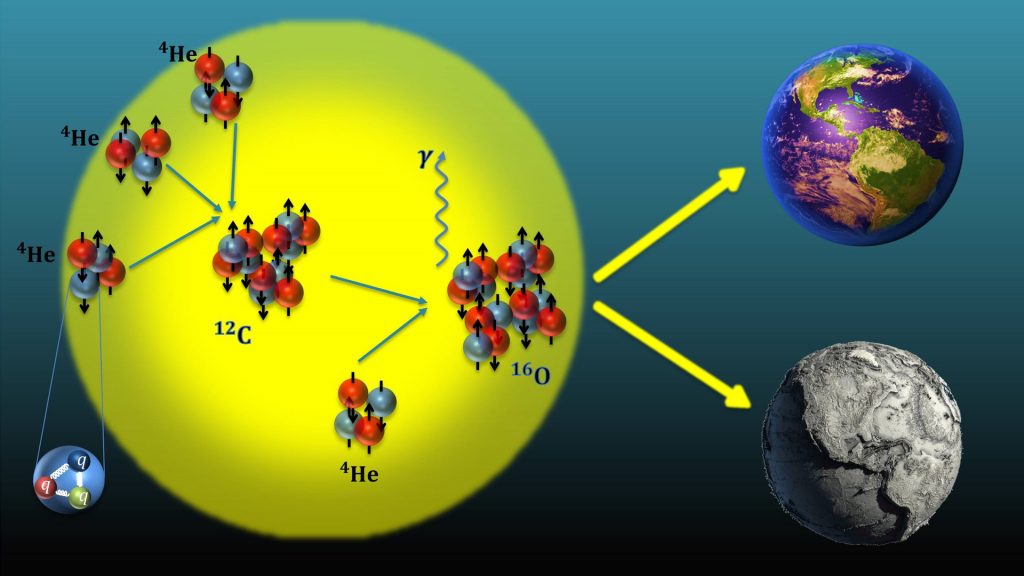
Fine-tunings in the production of carbon and oxygen in stars
The generation of the life enabling elements 12C and 16O proceeds through the famous triple-α process (three α-particles consecutively fuse to generate carbon) and the subsequent non-resonant capture of another a-particle in carbon. The first process is enhanced by proceeding through the “Hoyle state”, a resonance with spin zero and positive parity just 7.7 MeV above the ground state of 12C. This resonant behaviour is further magnified by the strong temperature dependence of the triple-a process at stellar temperatures. Another fine-tuning in the triple-α process is the closeness of the 8Be binding energy to the 2α threshold, which determines the rate of the first fusion process in this reaction chain. In fact, beryllium is unbound but has a rather long life-time, which allows for the capture of a third a-particle before it decays in a dense stellar environment.
However, using nuclear lattice EFT, it is possible that these two fine-tunings are correlated, that is, if one detunes the closeness of the 3α-threshold to the Hoyle state, one also upsets the closeness of the 8Be ground state energy to the 2α-threshold. It thus suffices to consider in detail one of these two conditions. Investigating the reaction rate as a function of the average light quark mass and the electromagnetic fine-structure constant requires precision input from lattice QCD. This provides hadron masses and couplings at varying quark masses, as well as sophisticated stellar simulations of the production of carbon and oxygen in stars, which is in particular sensitive to the metallicity Z of the stars, where Z = 0.2 is the solar metallicity and Z = 10-4 for older and heavier stars. In the first type of stars, variation of the quark masses below one percent are required to uphold the resonance condition (i.e. keeping the Hoyle state close to the 3α-threshold), whereas in low-metallicity stars, the production of 16O is the most constraining factor, allowing for quark mass changes up to five percent. It is important to remark that these new calculations exclude a scenario with no fine-tuning whatsoever. Interestingly, the triple-a reaction sets stringent limits on the aforementioned θ-parameter of QCD. A sufficient amount of carbon and oxygen is only produced when of θ < 0.1, so a universe with such a value of θ will most probably look like the one with θ = 0 (such as our own universe). Finally, it should be noted that an ab initio calculation of the so-called holy grail of nuclear astrophysics, the process α + 12C → 16O + γ at astrophysical energies, also for varying fundamental parameters, is in reach using nuclear lattice EFT.
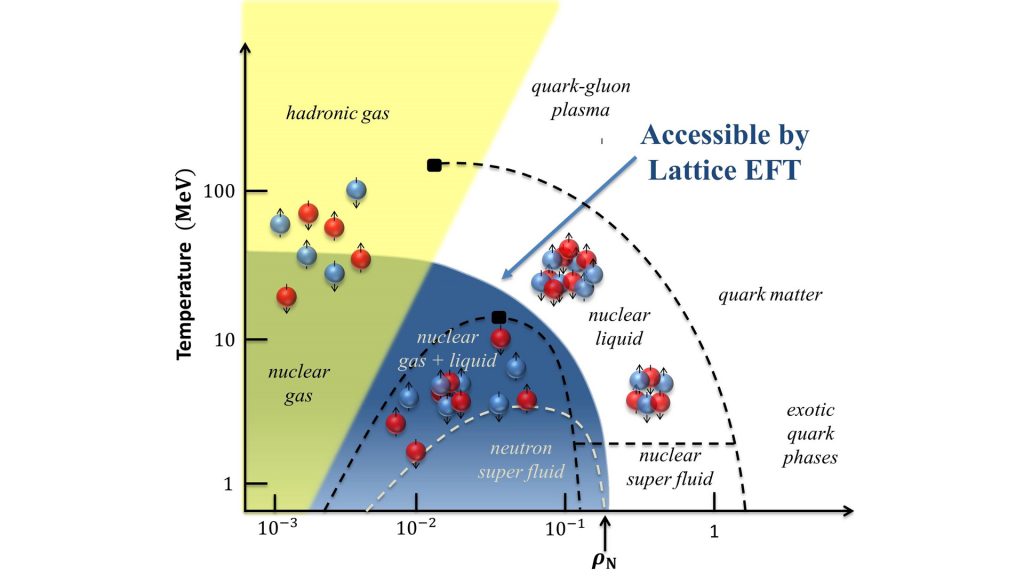
The nuclear equation of state
Another important quantity is the equation of state (EoS) of neutron matter. This has been under scrutiny because of the observation of gravitational waves from neutron star mergers. The precise spectrum of the emitted gravitational waves is very sensitive to the EoS, and it is thus predictions must be precise. Again, for a long time such calculations have been rather model-dependent, but this changed with the advent of consistent chiral two- and three-nucleon forces. Presently, a significant area of research is the role of three-nucleon forces and the inclusion of strange quarks, which set stringent limits on the upper mass a neutron star can have. Concerning the EoS, recent progress in nuclear lattice EFT is remarkable, because the algorithm used to calculate the EoS is many thousand times faster than previously existing methods, enabling for the first time, the calculation of the liquid-gas transition in nuclear matter with quantified uncertainties and the ab initio calculation of the density and temperature dependence of nuclear clustering as measured in heavy-ion reactions. Furthermore, chiral EFTs are being developed for hyperon-nucleon and hyperon-hyperon interactions. This allows scientists to investigate the third direction of the nuclear chart. Here, due to the scarcity of scattering data, the analysis of spectra of hypernuclei, i.e. nuclei in which one (or two) nucleon(s) is (are) replaced by one (or two) hyperon(s), plays a significant role in understanding these fundamental forces. There is ongoing worldwide activity to measure more hypernuclear spectra, which is improving the rather sparse data base. The analysis of this data using forces derived from chiral nuclear EFT will eventually let us answer the question of what role strange quarks really play inside neutron stars and other compact objects.

Cooperation and support
These theoretical developments require on the one hand intensive collaborations between scientists from various universities and research centres worldwide, as well as the use of high-performance computing facilities, such as provided by the Jülich Supercomputing Centre. This work is supported by the German Science Foundation (DFG) through funds provided to the Sino-German Collaborative Research Centre “Symmetries and the Emergence of Structure in QCD” (Project-ID 196253076 – TRR 110), by VolkswagenStiftung (Grant No. 93652) and by the Chinese Academy (CAS) President’s International Fellowship Initiative (Grant No. 2018DM0034).








